cs236 7-8장 Normalizing Flow Models

Generative model 복습을 위해 CS236 강의를 듣고 정리해보고자 한다.

피피티는 아래 페이지를 참고하면 된다.

https://deepgenerativemodels.github.io/

 

※ PPT의 내용 정리와 더불어 같이 보면 좋을 자료들을 정리했습니다. 강의를 보고 이해한대로 작성했기 때문에 부정확한 내용이 포함되어 있을 수 있음을 알려드립니다. 또한 참고한 모든 블로그와 유튜브는 출처(Reference)에 있습니다.

 

※ Normalizing Flow models 중 NICE, RealNVP, Glow 논문에 대한 리뷰는 아래 포스트에서 확인 가능합니다.

https://jjo-mathstory.tistory.com/entry/Flow-based-generative-modelNICE-Real-NVP-Glow-%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0

Flow-based generative model(NICE, Real NVP, Glow 논문리뷰)

 

Recap

앞 강의에서 배운 내용을 정리해보자.

우리는 Autoregressive Models과 Variational Autoencoders에 대해 배웠다. 

 

Autoregressive Models은 likelihood를 계산할 수 있으나, recursive한 구조때문에 학습이 매우 느린 단점이 있다.

VAE는 Autoregressive Model과 달리 빠른 학습이 가능하나, likelihood의 lower bound인 ELBO를 극대화해야 한다는 점에서 tractable한 likelihood 계산이 어렵다고 할 수 있다.

 

그렇다면 우리는 tractable한 likelihood식을 얻으면서도 빠른 모델을 찾을 수 밖에 없는데... 그것이 바로 Normalizing flow이다.

 

Change of Variable formula

증명 :

 

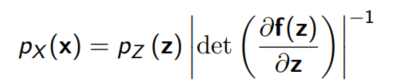
Change of variable 방법은 두 확률변수의 확률밀도함수를 하나의 식으로 쓸 수 있게 해준다. 변환 정도를 나타내기 위해 determinant term이 추가되는데, 이를 우리는 함수 $f$의 Jacobian matrix의 determinant, 즉 Jacobian determinant라고 부른다. 

 

여기서 우리가 눈여겨 보아야 할 점은 $x$와 $z$는 연속이며, $x$와 $z$의 차원이 같아야 한다는 점이다.

(그래야 invertible한 함수 $f$가 존재할 수 있다.)

 

Normalizing Flow models

Key idea behind flow models : Map simple distribution(easy to sample and evaluate densities) to complex distribution through an invertible transformation.

데이터 변수를 $X$로, 잠재 변수를 $Z$로 두고, 둘 사이의 invertible한 함수 $f$를 생각해보자. 

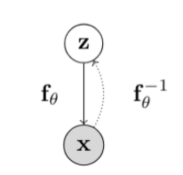
Change of variable을 사용하면 marginal likelihood $p(x)$는 다음과 같이 주어진다.

Normalizing Flow에서 각각의 단어가 의미하는 바는 아래와 같다.

 

Normalizing : Change of variable gives a normalized density after applying an invertible transformation.

Flow : Invertible transformations van be composed with each other 

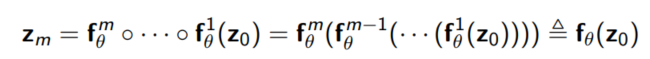
즉, invertible한 함수를 여러 층 쌓아 하나의 함수를 만들고, 이를 통해 단순한 확률밀도함수를 원하는 확률밀도함수로 변환하는 모델을 Normalizing Flow라고 할 수 있다.

 

$z_0$가 가우시안 분포를 따른다고 가정하고 $M$번째 변수가 x라고 가정하면 아래와 같이 변환이 가능하다.

 

예시) 가우시안 분포에서 샘플 분포로

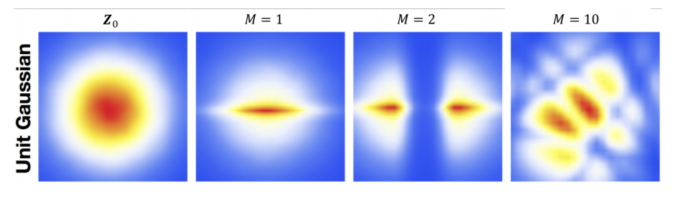
가우시안 분포가 변해가는 과정

 

Learning and Inference

likelihood를 최대화하는 과정을 통해 학습이 가능하며 inverse mapping을 통해 sampling을 할 수 있다.

여기서 우리는 $Z$의 분포를 쉽게 구할 수 있어야 학습하기도 편하며, 샘플링하기도 편하기 때문에, $Z$의 분포는 비교적 단순한 분포를 상정한다.(주로 가우시안 분포 사용)

 

또한 $f$와 $f^{-1}$ 도 likelihood를 계산하거나 sampling을 함에 있어서 단순해야 한다.

$f^{-1}$가 계산하기 쉽다는 말은 $f$의 jacobian determinant가 계산하기 쉽다는 말로, 행렬의 determinant가 계산하기 쉬워야 한다는 말이다.

 

일반적으로 함수의 determinant 계산은 $O(n^3)$로 알려져 있는데, 우리는 여기에 여러 조건을 추가해 계산을 단순화할 것이다. 가장 대표적인 예로는 우리의 jacobian matrix $f$를 triangular matrix나 diagonal matrix로 만드는 것이다.( 이 경우 $O(n)$의 계산이 필요하다. 왜냐하면 대각선에 있는 원소들만 모두 곱하면 되기 때문이다!)

 

어떠한 함수를 $f$를 고르는지에 따라 그 방법론이 조금씩 달라지는데, $f$에 많은 제약을 줄 수록 모델의 퍼포먼스는 떨어지는 trade off가 발생하기 때문에 마냥 단순한 모델이라고 좋은건 아니다.

 

이제부터는 각 모델에서 어떤 $f$를 골라 모델을 발전시켰는지 살펴보고자 한다.

 

※ 참고(Normalizing Flow의 발전)

1. NICE(Nonlinear Independent Components Estimation)(Dinh et al., 2014) 

2. Real-NVP( Dinh et al., 2016)

3. IAF(Inverse Autoregressive Flow)(Kingma et al., 2016)

4. MAF(Masked Autoregressive Flow)(Papamakarios et al., 2017)

5. I-resnet(Behrmann et al, 2018)

6. Glow(Kingma et al, 2018)

7. MintNet(Song et al, 2019)

 

 

Planar flows(Rezende & Mohamed, 2016)

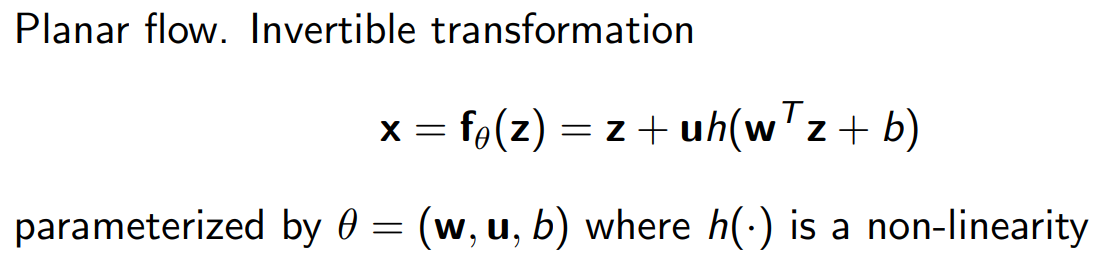
Planar flow에서는 $f_{\theta}$를 위와 같이 정의하였으며, Jacobian determinant는 아래와 같다.

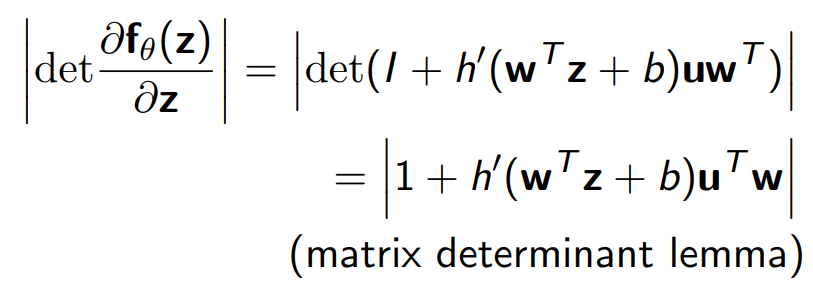
(여기서 h는 역함수가 존재해야 하며, h의 역함수가 존재할 수 있도록 $w, z, u$의 값이 설정되어야 한다.)

 

NICE(Dinh et al., 2014) 

additive coupling layer를 $f$로 골라 사용하였으며, $x$를 $x_{1:d}$와 $x_{d+1 : D}$ 파트로 나눠 함수를 적용한다.

Jacobian determinant는 1이 되며, Volume을 preserving하게 된다.

Volume을 늘리고 줄이면서 중요한 feature를 추출하기를 바라기 때문에, rescaling transformation을 추가로 고려한다. 

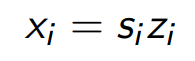
그러면 Jacobian determinant는 $s_i$들의 곱으로 바뀐다.

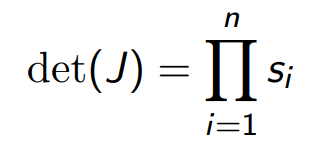
Real-NVP( Dinh et al., 2016)

affine coupling layer을 사용해 $f$를 정의한다. NICE와 마찬가지로 $x$를 두 개의 파트로 나눠 진행한다.

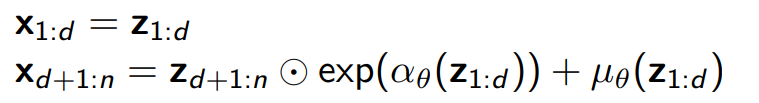
Jacobian determinant는 아래와 같다. $det(J)$는 1이 아니므로(1일 순 있으나 일반적으로는 1일 이유가 없음) volume을 preserving하던 성질이 더 이상 존재하지 않는다.

 

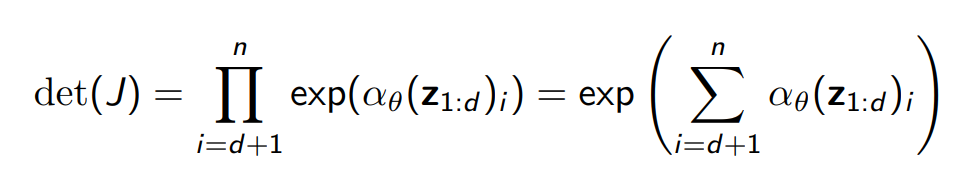
Continuous Autoregressive models as flow models

Autoregressive model를 flow model의 관점에서 볼 수 있다. 아래와 같이 Gaussian autoregressive model이 주어져 있다고 가정하자. 

위 모델을 $\bold{z}$에서 $\bold{x}$로 보내는 invertible한 transformation이라고 본다면 일종의 flow 모델로 생각해볼 수 있다.

 

Autoregressive model을 flow model로 보는 view를 이용해 MAF와 IAF를 설명할 수 있다. 사실 이 두 모델은 완전히 반대되는 성격을 가지고 있다고 할 수 있는데, MAF와 IAF의 단점을 극복한 모델이 Parallel Wavenet이라고 할 수 있다.

 

MAF(Papamakarios et al., 2017)

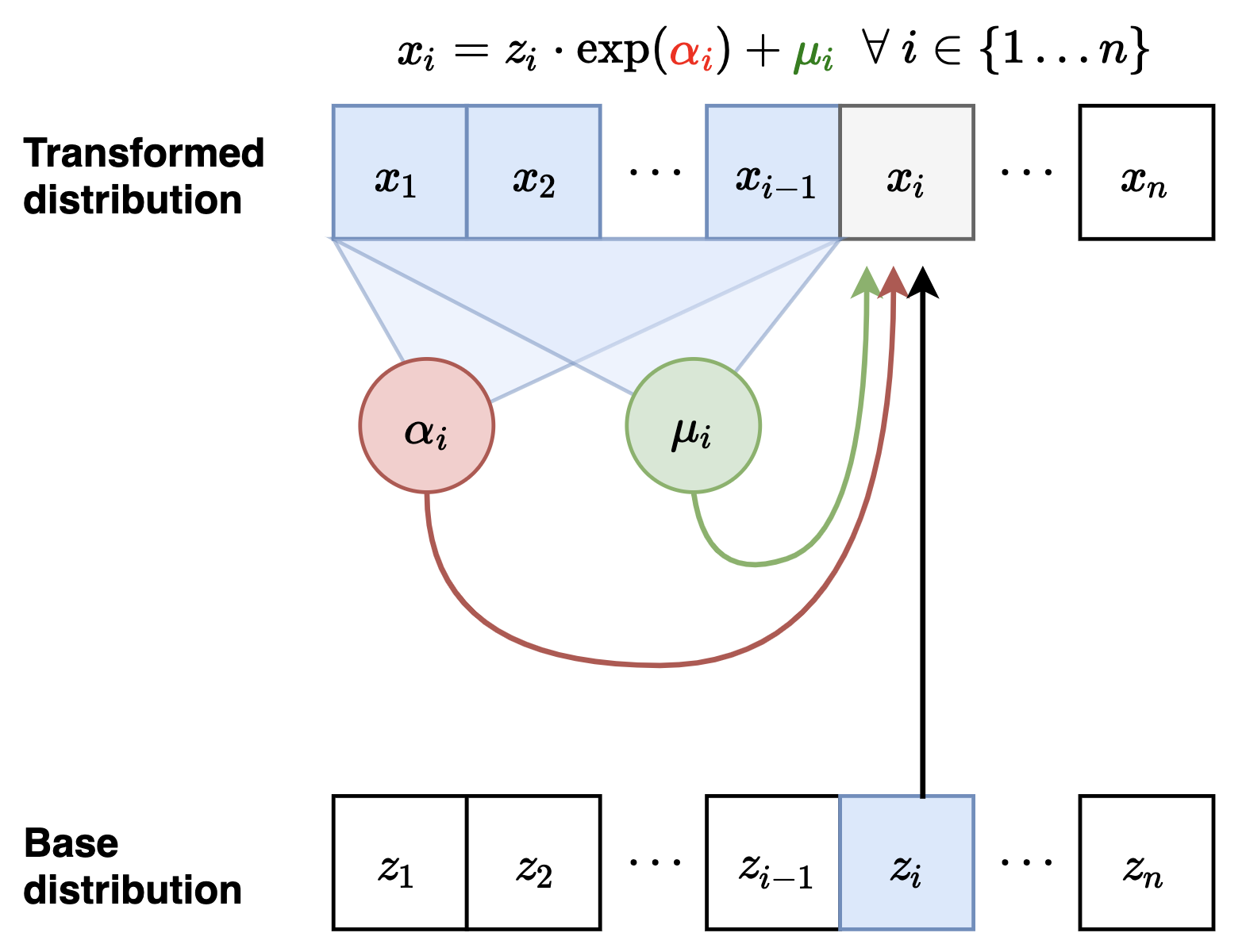
figure adapted from Eric Jang's blog

$\alpha$와 $\mu$가 $x$에 의해 결정된다는 사실을 눈여겨 보자. 

 

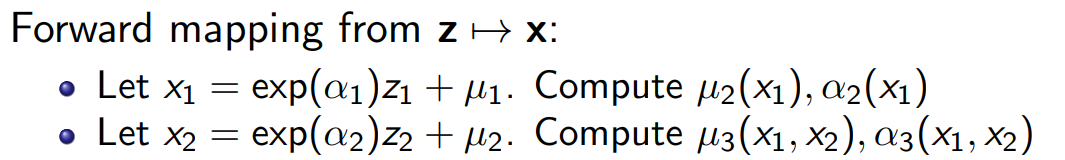
$z \rightarrow x$일 때, 즉 샘플링을 진행할 때 $\alpha$와 $mu$가 차례차례 결정된다는 사실을 알 수 있다.\

따라서 MAF에서는 Sampling이 느리다.

반대로, $x \rightarrow z$일 때는 $\alpha$와 $\mu$가 병렬적으로 계산이 가능하기 때문에 inverse mapping의 계산 속도는 $z \rightarrow x$ 방향보다 빠르다.

MAF : Sampling is sequential and slow(like autoregressive) : O(n) time

IAF(Inverse Autoregressive Flow)(Kingma et al., 2016)

IAF는 MAF와는 반대로 $\alpha$와 $\mu$가 $z$에 의해 결정된다. 

MAF와 다르게 sampling이 병렬적으로 진행될 수 있기 때문에 sampling이 빠르다는 장점이 있다.

\

다만 그 반대 변환(inference)이 순차적이기 때문에 $z$를 만드는데 오랜 시간이 걸린다.

IAF: Fast to sample from, slow to evaluate likelihoods of data points

IAF = inverse of MAF

☞ IAF is inverse of MAF

즉, MAF의 forward transformation은 IAF의 inverse transformation이며, 둘은 일종의 inverse 관계에 있다고 할 수 있다.

	MAF	IAF
Sampling	slow	fast
Likelihood Evaluation	fast	slow

 

이 외에도 normalizing flow는 모델의 제약조건을 약화하는 방향으로 발전해나갔다.

- Parallel wavenet(Oord, Aaron, et al. 2018)

- Mintnet(Song et al, 2019)

- Gaussian flows(Meng et al, 2020)

 

(Mintnet까지 겨우 읽긴 했는데 정리할 엄두가 나질 않아 빠르게 패스하려고 한다. 강의도 IAF, MAF까지만 자세히 다루고 그 이후의 모델은 빠르게 훝고 지나간다)

 

Summary

1. Transform simple distributions into more complex distributions via change of variables

2. Jacobian of transformations should have tractable determinant for efficient learning and density estimation

3. Computational tradeoffs in evaluating forward and inverse transformations