CS236 4장 Maximum Likelihood Learning

Generative model 복습을 위해 CS236 강의를 듣고 정리해보고자 한다.

피피티는 아래 페이지를 참고하면 된다.

https://deepgenerativemodels.github.io/

Stanford University CS236: Deep Generative Models

 

 

※ PPT의 내용 정리와 더불어 같이 보면 좋을 자료들을 정리했습니다. 강의를 보고 이해한대로 작성했기 때문에 부정확한 내용이 포함되어 있을 수 있음을 알려드립니다. 또한 참고한 모든 블로그와 유튜브는 출처(Reference)에 있습니다.

 

Setting

우리가 알고자 하는 확률밀도함수를 $P_{data}$로 정의하자. $P_{data}$ 에서 m개의 샘플을 추출해 데이터셋 $D$을 만들자. 여기서 우리는 각각의 샘플들이 I.I.D(independent and identically distributed)라고 가정할 것이다. 

우리의 목표는 model 집합 $M$을 이용해 좋은 모델을 고르고 $P_{data}$을 잘 학습하는 것이다.

 

KL-divergence

KL divergence를 알기 전에 기본적인 정보이론(entropy, cross entropy)도 함께 알아보자. 

 

Entropy : 최적의 전략 하에서 그 사건을 예측하는데 필요한 질문의 갯수로 entropy H가 감소한다는 의미는 정보량이 줄어든다는 것으로 볼 수 있다.  모든 사건의 발생 확률이 동일할 때 Entropy는 최대가 된다. 

 

$H = \sum (사건발생확률) * log_{2}(\frac{1}{사건발생확률}) =   -\sum_{i} p_i * log_{2}(p_i)$

 

Cross entropy : 어떤 문제에 대해 특정 전략을 쓸 때 예상되는 질문 개수에 대한 기댓값으로 해당 문제에 대해 최적 전략을 썼을 때 Cross entropy가 최소가 된다. 즉, 확률분포로 된 어떤 문제 $p$에 대해 확률분포로 된 어떤 전략 $q$를 사용할 때의 질문 개수의 기대값이라고 할 수 있다.

 

$H(p,q) = \sum_{i}p_{i}log_{2}\frac{1}{q_i} = - \sum_{i}p_{i}log_{2}(q_i)$

$p_i$ : 목표 확률(참 값)

$q_i$ : 우리가 현재 학습한 확률  

• Binary classification의 cost function $-ylog\hat{y} - (1-y)log(1-\hat{y})$ 또한 cross entropy로 이해할 수 있다.
• Cross entropy는 log loss로 불리기도 하는데, 이유는 cross entropy를 최소화 하는 것과 log likelihood를 최대화 하는 것이 같기 때문이다. 또한 같은 이유로 cross entropy는 negative log likelihood로 불리기도 한다.

 KL divergence(Kullback Leibler divergence) : 두 확률분포의 차이를 계산하는데에 사용하는 함수로, 어떤 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링한다면 발생할 수 있는 엔트로피의 차이를 계산한다.

 

$KL(p||q) = H(p, q) - H(p) = \sum_{i}p_{i}log\frac{p_i}{q_i}$

• 특징 (1) $KL(p|q) >= 0$ 
• 특징 (2) $KL(p|q) \neq KL(q|p)$ → KL divergence는 distance metric가 아니다.

Jensen-Shannon divergence 

$JSD(p||q)$ = $\frac{1}{2} KL(p||M)$ $+$ $\frac{1}{2} KL(q||M)$

where $M = \frac{1}{2}(p+q)$

• 목표 분포$p(x)$를 학습 가능한 파라미터 $\theta$의 $q(x|\theta)$를 이용해 근사시킨다고 가정해보자. 우리는 $p(x)$와 $q(x|\theta)$사이의 KL divergence를 최소화 하는 $\theta$를 찾아야 한다.

$KL(p||q) \sim \frac{1}{N} \sum_{i}^{N}{-\log q(x_n|\theta) + \log p(x_n)}$

 

▶ Cross entropy minimize = KL Divergence minimize = negative log likelihood maximize

 Monte Carlo Estimation

log likelihoog를 최대화 하기 위해서는 독립적인 샘플을 뽑아 KL divergence를 최소화 하는 $\theta$를 찾아야 한다. 이때 많은 수의 샘플을 뽑아 평균을 구하는 수치해석적 기법으로 몬테카를로 시뮬레이션이 있다. 

 

몬테카를로 시뮬레이션은 3가지 성질을 가지고 있다. 

(1) Unbiased

(2) (By the law of large number) Convergence

(3) Variance reduces as the number of samples increase

편향되지 않았기 않고 수렴을 보장하며, 샘플을 많이 사용할 수록 분산이 작아지기 때문에 샘플을 늘려 평균의 좋은 예측치를 만들 수 있다.

Autoregressive Model에서 MLE problem 생각해보기

Autoregressive Model에서 MLE 문제를 생각해보자.

우선 $P_{\theta}(x)$는 과거의 노드들에 대한 conditional probability의 곱으로 나타낼 수 있다.

Likelihood 함수는 각각의 샘플 $x^{(j)}$에 대한 $P_{\theta}(x)$를 계산해 곱한 함수로 다음과 같이 표현이 가능하다.

여기서 우리의 목표는 Likelihood 함수가 최대가 되는 $\theta$를 찾는 것이다. Autoregressive Model은 과거 state에 대한 조건부 확률 곱이므로 추가적인 조건 없이 해당 식을 풀기 쉽지 않다.

 

$L(\theta, D)$를 최대화하는 $\theta$는 $\log{L(\theta, D)}$ 역시 최대화할 것이며, 이를 $l(\theta)$로 표현하자.

양 변에 로그 함수를 취하면 곱은 합으로 변하고, discrete하기 때문에 곱 안으로 log 함수가 들어갈 수 있다,

이제는 합으로 표현되어 있기 때문에 gradient of $l(\theta)$를 구하기 수월하다!

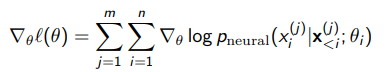
따라서 Gradient Descent를 수행해 $\theta$를 업데이트하여 $l(\theta)$를 최대로 하는 $\theta$를 찾을 수 있다.

이는 Non-convex optimization problem이지만 실제로 학습시키면 잘 작동하는 경향이 있다. 

※ i = 1 ~ n까지 고려해주는 이유 : 각각의 조건부 $p_{neural}(x_i|x_{<i}^{(j)}; \theta_i)$는 $\theta_i$를 공유하지 않는다면 i =i인 경우만 생각하면 되지만, 일부 모델(NADE, PixelRNN, PixelCNN 등)은 파라미터를 공유하기도 한다.

 

만약 $m = |D|$, 즉 샘플의 수가 크다면 $m \times \frac{1}{m}$을 곱해 다음과 같이 표현할 수 있다.

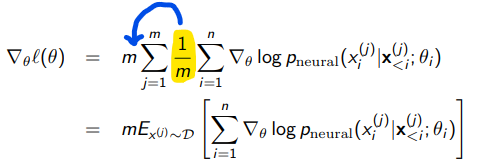
$\frac{1}{m}$은 j와 독립

 

gradient를 expectiation으로 표현함으로써 우리는 이제 gradient descent를 위해 몬테카를로 시뮬레이션이 가능하다. 

전체 샘플에 대해  gradient를 구하는 대신 일부 샘플 셋에 대한 평균만 계산함으로써 gradient를 업데이트할 수 있다. 

 

Empirical Risk and Overfitting - Bias and Variance

Overfitting을 방지하기 위해 hypothesis space of distribution에 제약 조건을 추가할 수 있다.

 

만약 제약이 너무 강할 경우, Loss를 최소화하지 못해 모델을 제대로 표현하지 못할 위험이 있는데 이러한 한계를 우리는 bias라고 부른다. bias가 높을 경우 모델이 학습 데이터의 패턴을 잘 잡아내지 못하며 지나치게 단순화된 결정을 내린다. 또한 만약 제약이 너무 약할 경우, 모델은 train data에 대해서만 잘 작동하고, test data에 대해서는 작동하지 않을 가능성이 있는데, 이러한 한계는 variance라 부른다. variance가 높을 경우 모델이 학습 데이터에 매우 민감하여 데이터의 작은 변화에도 크게 반응한다. 

 

bias : 모델이 학습 데이터의 패턴을 잘 학습하지 못하는 정도

variance : 모델이 학습 데이터에 얼마나 민감한지 나타내는 정도

 

따라서 hypothesis class를 결정함에 있어 bias-variance trade off는 항상 발생한다. bias를 줄이다보면 variance가 늘어나고, variance를 신경쓰다보면 bias가 줄어들기 때문이다

 

How to avoid overfitting?

오컴의 면도날(Occam's Razor) : 데이터를 설명하는 가장 단순한 모델을 선호하는 원칙이다. 만약 성능이 비슷한 두 모델이 있다면 우리에게 더 좋은 모델은 파라미터의 수가 더 적거나 파라미터의 크기가 작은 모델이다. 

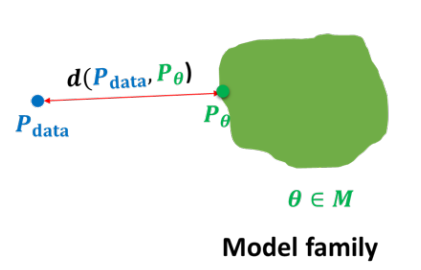
즉, 우리는 초록색 면적을 줄이면서도 $P_data$를 잘 설명하는 모델을 찾으려고 노력하는 것이다!

 

Regularization(정규화)

$objective(x, M) = loss(x, M) + R(M)$

where $loss(x, M)$ : loss function,

$R(M)$ : regularization term that penalizes the complexity of the model M

 

정규화의 종류

(1) L1 정규화(Lasso) : $R(M) = \lambda \sum_{j = 1}^{p} |w_j|$

sparsity를 유도하여 일부 계수를 정확히 0으로 만들어 특성 선택(feature selection)의 효과를 가져올 수 있다. 

(2) L2 정규화(Ridge) : $R(M) = \lambda \sum_{j = 1}^{p} w_{j}^2$

sparsity를 유도하지는 않지만, 계수를 작게 유지하려고 노력한다.

(3) Elastic Net : $ R(M) = \lambda_{1} \sum_{j = 1}^{p} |w_j|$ + $\lambda_{2}$ $\sum_{j = 1}^{p}$  $w_{j}^2 $

L1과 L2 정규화의 조합으로 두 정규화의 중간 성질을 가지고 있다. 

 

여기서 $\lambda$는 벌칙의 강도를 조정하는 매개변수로 $\lambda$값이 클수록 벌칙이 커지며, 더 단순한 모델이 된다. 

Reference

[1] Entropy : https://hyunw.kim/blog/2017/10/14/Entropy.html

[2] Cross entropy : https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html

[3] KL divergence : https://hyunw.kim/blog/2017/10/27/KL_divergence.html