cs236 11-12장 Energy-Based Models(EBM)

Generative model 복습을 위해 CS236 강의를 듣고 정리해보고자 한다.

피피티는 아래 페이지를 참고하면 된다.

https://deepgenerativemodels.github.io/

 

※ PPT의 내용 정리와 더불어 같이 보면 좋을 자료들을 정리했습니다. 강의를 보고 이해한대로 작성했기 때문에 부정확한 내용이 포함되어 있을 수 있음을 알려드립니다. 또한 참고한 모든 블로그와 유튜브는 출처(Reference)에 있습니다.

 

이번 강의에서는 Energy-Based Models에 대해 공부해보고자 한다. Energy-Based Moels는 아래와 같은 장점을 지니고 있는 모델이다.

1. Very flexible model architectures
2. Stable training
3. Relatively high sample quality
4. Flexible composition

Parameterizing probability distributions

확률변수 $p(x)$를 생각해보자. $p(x)$는 아래 두 가지 성질을 만족해야 한다.

• $p(x) \geq 0$
• $\Sum_{x}p(x) = 1$ or $\int p(x)dx = 1$ 

$p(x)$를 양수가 되게끔하는 함수는 매우 다양하다.(제곱을 하거나, 절대값을 취하거나, exp을 취하거나 등등) 

하지만 $p(x)$의 합이 1이 되게끔 하는 것은 생각보다 어려운데, 그렇기 때문에 우리는 함수 $p(x)$를 normalize시킨다.

위와 같이 정의한 $p_{\theta}(x)$는 적분값(또는 단순합)의 값이 1이 된다는 장점이 있으나, $Z(\theta)$를 analytic하게 구할 수 있는 함수 $g(x)$를 고르는 순간 $p(x)$의 구조에 많은 제약이 생긴다. 

 

우선 우리는 넓은 범위를 커버하기 위해 exponential $f(x)$를 생각할 것이다. 위와 같이 정의하게 되면 물리학적인 관점에서 $-f_{\theta}(x)$는 energy가 된다는 사실을 알 수 있다. 직관적으로 $x$위치에서 작은 energy를 갖는 $x$를 우리는 선호한다.(확률이 높기 때문)

 

장점 : 함수 $f$에 대한 제약이 없어지므로 구조가 상당히 유연해진다

단점 : $p_{\theta}(x)$로부터의 샘플링, 계산, 최적화가 복잡해지며, feature learning이 어려워진다.

 

위와 같이 정의할 경우에도 우리는 $Z(\theta)$를 쉽게 계산하는 방법을 알지 못한다. 다만 두 데이터 $x$와 $x'$에 대해 $p(x)$와 $p(x')$을 비교하는 것은 $Z(\theta)$가 필요하지 않다. 즉, $p(x)$와 $p(x')$ 중 좀 더 확률이 높은 데이터를 알 수 있다는 점이다!

Example) Restricted Boltzmann machine(RBM)

RBM : enery-based model with latent variables

여기서 $Z$는 아래와 같이 계산된다. $n$와 $m$이 커지면 $Z$의 계산도 늘어나기 때문에 $p_{W, b, c}$를 계산하는 것은 차원이 커질수록 어려운 일임을 알 수 있다.

※ RBM을 쌓아 만든 모델이 Deep Boltzmann Machines(DBM)이며, deep generative model의 초창기 모델 중 하나다. 

 

Training Intuition

 

우리는 $\theta$를 바꾸므로써 분자를 증가시켜 확률을 키우는 방향으로 $\theta$를 학습하면 된다고 생각하지만, 실제로 $\theta$가 변하면 $Z(\theta)$도 변한다는 사실을 간과해서는 안된다. 따라서 우리는 분모 $f_{\theta}(x)$는 늘리되, $Z(\theta)$는 줄이는 방향으로 학습을 진행해야 한다.

 

📢 여기서 우리는 학습을 위해 $Z(\theta)$를 Monte Carlo estimate를 이용해 계산할 것이다.

 

Constrastive divergence algorithm : RBM같은 Energy-Based Models의 학습을 효율적으로 수행하기 위한 알고리즘으로 아래와 같이 학습힌다.

증명)

 

그렇다면 샘플링은 어떻게 진행할까?

 

우리는 샘플 $x$에 대한 확률을 모르기 때문에 샘플링하는데 어려움을 겪는다. 이럴때 Markov Chain Monte Carlo(MCMC)방법론을 사용하는데, 두 개의 샘플 $x$와 $x'$을 비교할 수 있다는 아이디어에서 시작한다.

MCMC는 수렴하는데 상당히 오래 걸린다는 단점이 있는데, score function을 사용해 아래와 같이 Langevin MCMC를 도입할 수도 있다.

 

참고로 score function은 아래와 같이 정의하며, $Z(\theta)$와 독립적이라는 사실을 눈여겨 보자.

Metropolis-Hastings MCMC

Energy-Based Models의 Result

 

Score function

위에서 논의했던 score function으로 되돌아오자. score function의 정의는 다음과 같다. 

※ score function이 $Z(\theta)$와 독립이라는 점을 주목하자.

score function에서는 이제 함수 대신 함수의 gradient를 중심으로 본다. 

Fisher divergence는 다음과 같이 정의한다.

Score matching

score matching은 $p_{data}$와 $p_{\theta}$를 matching시킨다는 의미는 score를 matching시킨다고 볼 수 있으며, 우리의 목표는 $p_{data}$와 $p_{\theta}$의 Fisher divergence를 최소화 하는 방향으로 $\theta$를 학습한다고 할 수 있다.

]

증명)

Score matching을 수행하는 방법은 아래와 같다. Score matching 기법을 이용하면 앞서 소개한 MCMC 기법으로 샘플링을 하지 않는다는 점이 장점이지만, 사실 Hessian의 trace를 구하는 것 역시 차원이 커지면 비싼 계산이기 때문에 적절하지 않다. 

따라서 Hessian의 trace를 계산하지 않기 위해 우리는 앞으로 Denoising score matching(Vincent, 2010)과 sliced score matching(Song, 2019)에 대해 살펴보고자 한다. (다음 포스팅에서 확인 가능합니다)

 

Noise contrastive estimation(NCE)

Noise contrastive estimation은 EBM을 노이즈 분포와 대조하여 학습하는 방법으로 모델이 데이터 분포와 노이즈 분포를 구별할 수 있도록 학습시키는 방법이다. 

• Data distribution : $p_{data}(x)$
• Noise distribution : $p_n(x)$ (analytically tractable and easy to sample from)
• Training a discriminator $D_{\theta} in [0, 1]$ to distinguise between data samples and noise samples

objective function

Gan에서 배웠다시피, Optimal discriminator는 다음과 같다.

\

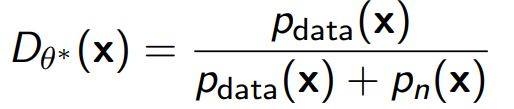
discriminator를 다음과 같이 두자.

그러면 Optimal한 discriminator는 다음 식을 만족하게 되며, $p_{{\theta}^{*}}(x) \sim p_{data}(x)$이도록 학습된다.

$p_{\theta}(x)$에서 우리는 $Z(\theta)$를 모르는 상황이기 때문에 이러한 방법론은 상당히 유용하며, 아래와 같은 식을 통해 $p_{{\theta}^{*}}(x)$를 얻을 수 있다.

또한 $Z(\theta)$가 $e^{f(x)$의 적분값이라는 조건을 만족시키는 것이 상당히 어려우므로 우리는 $Z(\theta)$를 하나의 학습 가능한 파라미터 $Z$로 보고 optimal한 $\theta$와 $Z$를 찾는 방향으로 학습한다.

이렇게 찾은 $Z$는 실제로도 optimal한 값인데, 왜냐하면 위 식 양변에 적분을 취했을 때의 합이 1이 되게끔 만족시키기 때문이다.

$Z$를 하나의 파라미터로 보고 discriminator의 식과 objective function을 다시 써보면 다음과 같다.

그리고 위 식의 discriminator를 objective function에 대입하면 아래와 같이 쓸 수 있다.

$log(exp(x)) = x$임을 이용해 log-sum-exp trick을 사용해 식을 다음과 같이 나타낼 수 있다.

 

※ log-sum-exp trick을 사용하면 로그 확률을 계산할 때 생기는 오버플로우와 언더플로우 문제를 방지할 수 있다.

예를 들어 $log(e^a + e^b)$ 계산에서 a와 b의 값의 차이가 매우 크다면(a>>b) 계산 결과는 $log(e^a)$와 같이 주어져야 하지만 컴퓨터의 수치 연산 과정에서 오버플로우 혹은 언더플로우가 발생할 수 있다. 따라서 log-sum-exp trick을 통해 $log(e^a + e^b) = a + log(1 + e^{b-a})$로 변형하여 계산하면 수치적 안정성을 개선할 수 있다.

 

NCE를 통한 EBM 학습 방법은 다음과 같다.

NCE와 GAN의 공통점

• 두 모델 모두 discriminator를 binary classification을 위해 사용
• likelihood-free model

NCE와 GAN의 차이점

• GAN은 adversarial training 또는 minimax optimizertion을 통해 학습하지만 NCE는 그렇지 아니함
• NCE는 noise distribution의 likelihood를 필요로 하지만 GAN은 prior에서 샘플링만 되면 됨
• NCE는 EBM을 학습하지만, GAN은 deterministic한 생성자를 학습함

Flow contrastive estimation

NCE에서는 Noise $p_n$을 사용해 샘플링을 용이하게 했으나, FCE에서는 $p_n$이 $p_{data}$에 가깝도록 골라 학습을 진행하였다. 여기서 $p_n$은 parametrized noise distribution with a normalizing flow model $p_{n, \phi}(x)$를 골랐다.

이때 parameterized discriminator는 다음과 같이 정의된다.

 

Adversarial training for EBMs

위와 같은 식 전개를 통해 log-likelihood의 upper bound를 얻을 수 있다.

 

Conclusion

Energy-Based Model은 모델의 제약이 없는 probabilistic model로 $Z(\theta)$를 계산하는데 어려움이 있어 이 점을 극복하기 위한 방향으로 모델이 발전되었다.

likelihood을 직접 계산하고 샘플링을 진행하는 것이 어려워 MCMC 방법론으로 샘플을 만들지만, 두 개의 데이터 샘플을 비교하는 일은 쉽게 한다. 

Maximum likelihood training은 contrastive divergence algorithm을 통해 진행하며, 각각의 알고리즘 과정에서 샘플링을 진행하기 때문에 학습이 느리다. 

이 점을 극복하기 위해 샘플링이 필요하지 않은 score mathing 기법과 noise contrastive estimation 기법이 새로이 제안되었으며, adversarial optimization 방법론도 고안되었다.

참고로 Energy-Based Model을 학습하기 위한 distance로서 우리는 contrasitve divergence와 Fisher divergence에 대해 살펴보았다.