-
VAE 논문 리뷰 ['13 arXiv] Auto-encoding variational bayes(Kingma, D.P. & Welling, M.)논문 리뷰/Generative Model 2024. 6. 28. 17:13
2013년도 Kingma, D.P. & Welling, M.의 Auto-encoding variational bayes 논문을 리뷰해보겠다. 이 논문은 정말 불친절한 논문이라고 생각이 드는데, cs236 5장과 6장 강의를 보지 않았다면 읽고 이해하는데 정말 많은 시간이 걸렸을 것이라고 생각한다. 배경지식이 없다면 VAE의 개괄을 설명하는 유튜브 강의나 블로그 글을 읽는 것을 추천한다.
사전지식
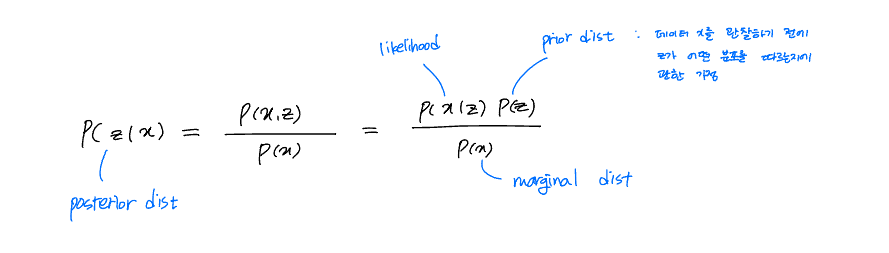
이 논문에서는 posterior distribution, prior distribution, likelihood에 대한 단어가 정의 없이 나오므로 용어를 숙지하는 것이 중요하다.
Setting

우리의 세팅은 위와 같다. $\theta$와 $z^{(i)}$는 알 수 없기 때문에 우리는 recognition model을 도입할 것이다.
* recognition model은 알고 싶은 함수를 모를 때 다른 함수로 근사하게끔 하는 모델을 말한다.

$\phi$와 $\theta$를 같이 학습함으로써 recognition model이 true posterior에 가까워지도록 한다.
ELBO
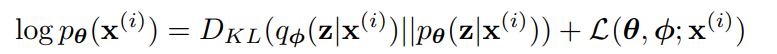
※ 유도하는 방법은 https://jjo-mathstory.tistory.com/entry/cs236-5-6%EC%9E%A5-Latent-Variable-ModelsVAEs 참고
여기서 $L(\theta, \phi; x^{(i)}$는 ELBO(Evidence Lower Bound)라고 부르며 우리는$D_{KL}$ term은 항상 양수이기 때문에 $L(\theta, \phi; x^{(i)}$는 $\log{p_{\theta}(x^{(i)}}$이다.

ELBO를 최대화하기 위해서는 gradient ascent method를 사용해야 한다. 그러기 위해서는 gradient를 계산할 수 있어야 한다.
ELBO 식을 자세히 보면 $\nabla_{\theta}L$는 쉽게 구해지지만, $\nabla_{\phi}L$를 구하기 까다롭다. $\nabla_{\phi}L$ 을 구하기 위해서는 reparametrization trick이 필요하다.
Reparametrization trick
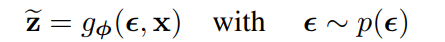
reparametrization trick이란 $z$를 보조 확률변수 $\epsilon$과 $g_{\ph}$를 이용해 다시 나타내는 방법이다.
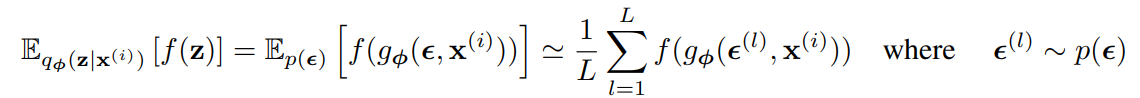
이 방법을 이용하면 $\nabla_{\phi}$를 구하기 간편해진다.(일종의 measure change technique)
그리고 이렇게 구한 variational lower bound를 통해 Stochastic Gradient Variational Bayes(SGVB) estimator를 구할 수 있다. ($\tilde{L^A}$ 를 SGVB의 first version이라고 부르자)
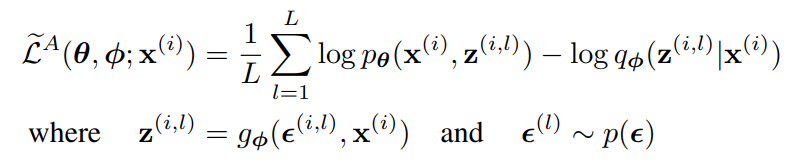
만약 $q_{\phi}$와 $p_{\theta}$의 식을 통해 $D_{KL}$ term을 직접 계산할 수 있다면 Monte-Carlo simulation을 통하지 않고 직접 계산할 수 있다. ($\tilde{L^B}$ 는 SGVB의 second version이라고 부른다.)
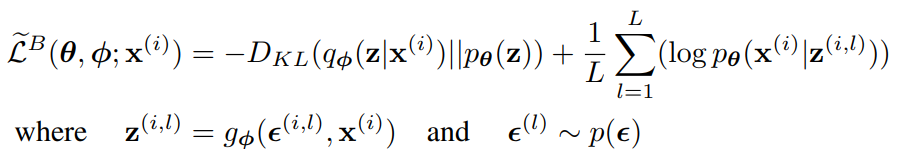
즉, SGVB estimator를 통해 ELBO를 추정하며, 우리의 목적은 $\theta$와 $\phi$를 잘 조정해서 ELBO가 최대가 되도록 하는 것이다!(ELBO의 직접 계산은 어려우니 SGVB estimator를 통하는 것 뿐이다. 왜냐면 SGVB는 ELBO의 unbiased estimator이기 때문이다.)
ELBO의 의미

첫번째 식(KL divergence term) : regularizer
두번째 식(expectation term) : negative reconstruction error
* 두번째 식을 negative reconstrubtion error라고 부르는 이유 : min(Loss) = min(-ELBO) = min(KL - E)
AEVB algorithm

Example
$p_{\theta}(z) = N(z; 0, I)$이고, $p_{\theta}(x|z)$를 multivariate Gaussian 또는 Bernoulli distribution이라고 하자. 또한 아래와 같이 가정하자.
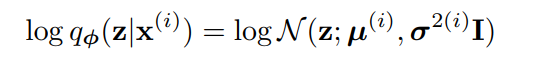
주어진 $x^{(i)}$에 대해 $z^{(i, l)} = g_{\phi}(x^{(i)}, \epsilon^{(l)}$을 다음과 같이 reparametrize하자.
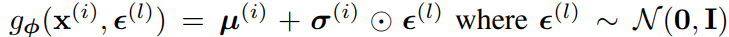
그러면 SGVB의 second version을 사용할수 있다.($p_{\theta}(z)$와 $q_{\phi}(z|x)$가 모두 Gaussian이기 때문)
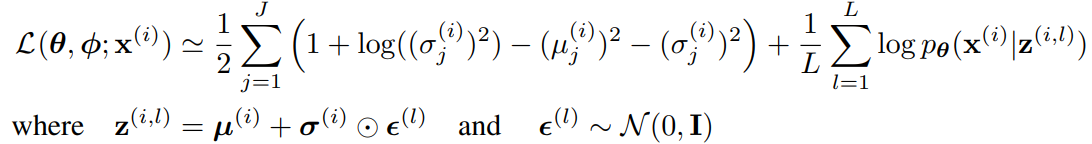 더보기
더보기증명 :
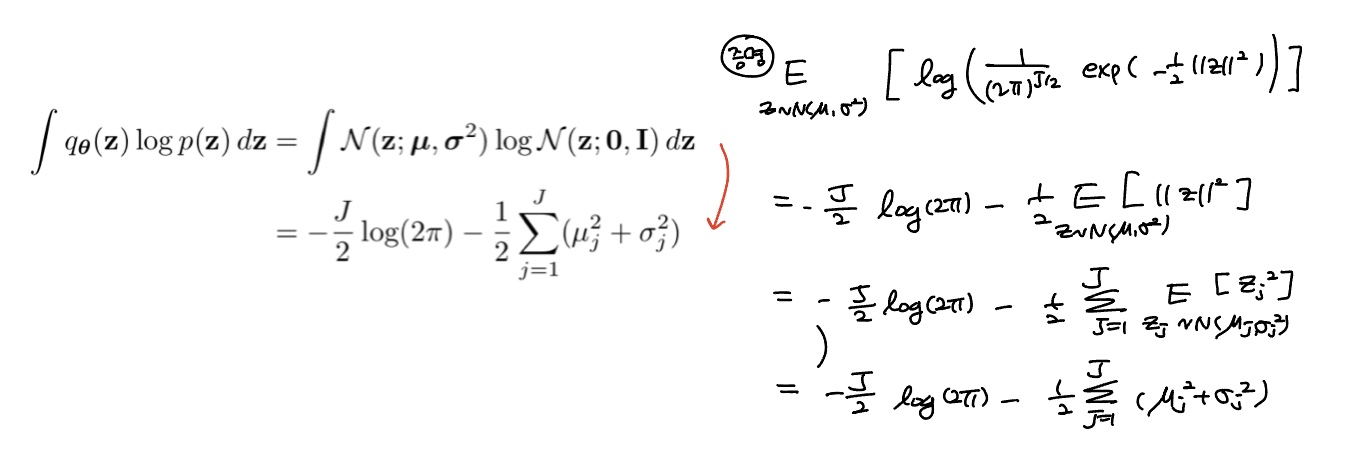
구현 코드
import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader from torchvision import datasets, transforms import matplotlib.pyplot as plt # 하이퍼파라미터 설정 batch_size = 128 learning_rate = 1e-3 num_epochs = 20 latent_dim = 20 # CUDA 사용 가능 여부 확인 device = torch.device("cuda" if torch.cuda.is_available() else "cpu") print(f"Using device: {device}") # 데이터 로더 설정 transform = transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,)) ]) train_dataset = datasets.MNIST(root='./data', train=True, transform=transform, download=True) train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True) # VAE 모델 정의 class VAE(nn.Module): def __init__(self): super(VAE, self).__init__() # 인코더 self.encoder = nn.Sequential( nn.Linear(28 * 28, 400), nn.ReLU(), nn.Linear(400, 2 * latent_dim) # 잠재 변수의 평균과 로그 분산 ) # 디코더 self.decoder = nn.Sequential( nn.Linear(latent_dim, 400), nn.ReLU(), nn.Linear(400, 2 * 28 * 28) # 출력 평균과 로그 분산 ) def encode(self, x): h = self.encoder(x) mu, logvar = torch.chunk(h, 2, dim=1) return mu, logvar def reparameterize(self, mu, logvar): std = torch.exp(0.5 * logvar) eps = torch.randn_like(std) return mu + eps * std def decode(self, z): h = self.decoder(z) mu, logvar = torch.chunk(h, 2, dim=1) return mu, logvar def forward(self, x): mu, logvar = self.encode(x.view(-1, 28 * 28)) z = self.reparameterize(mu, logvar) recon_mu, recon_logvar = self.decode(z) return recon_mu, recon_logvar, mu, logvar # 손실 함수 정의 def loss_function(recon_mu, recon_logvar, x, mu, logvar): # 재구성 손실 (가우시안 로그 가능도) recon_x = recon_mu + torch.exp(0.5 * recon_logvar) * torch.randn_like(recon_logvar) BCE = -0.5 * torch.sum(recon_logvar + ((x.view(-1, 28 * 28) - recon_mu) ** 2) / torch.exp(recon_logvar)) # KL 발산 KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp()) return BCE + KLD # 모델, 옵티마이저 설정 model = VAE().to(device) optimizer = optim.Adam(model.parameters(), lr=learning_rate) # 학습 루프 for epoch in range(num_epochs): model.train() train_loss = 0 for batch_idx, (data, _) in enumerate(train_loader): data = data.to(device).float() optimizer.zero_grad() recon_mu, recon_logvar, mu, logvar = model(data) loss = loss_function(recon_mu, recon_logvar, data, mu, logvar) loss.backward() train_loss += loss.item() optimizer.step() if batch_idx % 100 == 0: print(f'Epoch {epoch}, Batch {batch_idx}, Loss: {loss.item() / len(data)}') print(f'====> Epoch: {epoch} Average loss: {train_loss / len(train_loader.dataset)}') # 학습된 모델 저장 torch.save(model.state_dict(), 'vae.pth')'논문 리뷰 > Generative Model' 카테고리의 다른 글