-
MAF, IAF 등의 논문을 읽다보면 자주 나오는 MADE 논문에 대해 정리해볼 예정이다.
이 논문의 아이디어는 매우 심플한데, Autoregressive model을 구현하기 위해 sequential한 계산을 하는게 아니라 하나의 마스크를 사용하는 것이다. 개인적으로는 아이디어가 매우 번뜩이는 논문이라고 생각한다(모든 논문이 다 그렇게 보이긴 하지만..)
[15' PMLR] MADE(Masked Autoencoder for Distribution Estimation)(Germain et al.)
더보기Our method masks the autoencoder’s parameters to respect autoregressive constraints:
each input is reconstructed only from previous inputs in a given ordering
Introduction
이 논문에서는 mask를 이용해 output이 주어진 input에 대해 autoregressive한 성질을 갖게 한다. 또한 multiple ordering을 사용해 학습이 더 잘 될 수 있도록 돕는다.
예시)
input $x = (x_1, x_2, x_3)$이고, output $y = (y_1, y_2, y_3)$라고 하자. (☜벡터가 아니라 입력이 들어오는 순서)
autoregressive한 성질을 갖기 위해서는 현재 state가 과거 input에 대해서만 연관되어 있어야 하므로 $y = f(x_t; x_{<t})$의 꼴로 나타나야 한다.
즉, $y_1 = f(x_1)$, $y_2 = f(x_2; x_1)$, $y_3 = f(x_3; x_1, x_2)$으로 적을 수 있다.
또한 input을 1, 2, 3의 순서가 아니라 순서를 바꿔서 multilple ordering인 경우도 생각해 볼 수 있다. 예를 들어 input의 순서가 3, 2, 1로 들어온 경우를 1, 2, 3으로 보고 계산하는 식이다.
이렇게 하는 이유는 $p(x)$를 아래와 같이 conditional proability의 곱 꼴로 쓰고 싶기 때문이다.

자세한 내용은 아래 글 참고↓
https://jjo-mathstory.tistory.com/entry/CS236-3%EC%9E%A5-Autoregressive-Models-%EC%A0%95%EB%A6%AC
Autoencoders
$t = 1, 2, ...., T$일 때 학습 데이터로 T개의 $x_t$가 있다고 가정하자. 편의상 D차원 $x$에 대해 각각의 원소는 0 또는 1일 갖는다고 가정하자. 우리는 아래와 같이 $\hat{x}$를 reconstruction한다,

위 autoencoder를 학습하기 위해 우리는 cross-entropy loss를 선택할 것이다.

$\hat{x}$이 $x$에 가깝도록 학습하는 위 과정을 우리는 autoencoder라고 한다. 여기서 $p(x_d = 1) = \hat{x_d}$로 보면 log-likelihood function 형태를 갖춘다는 것을 알 수 있다.
autoencoder의 장점은 구조의 flexibility다. 우리는 hidden layer를 여러겹 추가하므로써 구조를 더 다양하게 만들 수 있다.
다만 autoencoder가 배울 수 있는 representation이 한정된다는 점은 단점으로 꼽힌다. hidden layer가 input을 완전히 외워버리므로서 output을 추정하게끔 학습될 여지가 많기 때문이다.
또한 우리가 위에서 선택한 cross-entroypy loss은 완전한 log likelihood function이 아니다.

모든 x에 대해 확률이 1로 학습될 수 있어 normalize되었다고 할 수 없다. Distribution Estimation as Autoregression
모든 확률은 아래와 같이 nested conditionals의 곱으로 표현이 가능하다.

$p(x_d = 1 | x_{<d}) = \hat{x_d}$, $p(x_d = 0 | x_{<d}) = 1 - \hat{x_d}$로 정의하면 valid negative log-likelihood 형식으로 작성 가능하다.
※ 앞에서는 $p(x_d = 1) = \hat{x_d}$로 정의했음을 기억하자.

우리는 $\hat{x_d}$가 $x_{<d}$에만 의존하고 $x_{\geq d}$에는 의존하지 않는 성질을 autoregressive property라고 한다.
Masked Autoencoders
Goal :How to modify the autoencoder so as to satisfy the autoregressive property.
아이디어는 매우 심플하다. autoregressive property를 만족하기 위해서는 $\hat{x_d}$가 $x_{<d}$에만 의존하고 $x_{\geq d}$에는 의존하지 않아야 한다. 즉 $\hat{x_d}$를 계산할 때 $x_{\geq d}$의 연결을 끊으면 된다.
연결을 끊기 위해서는 $\hat{x_d}$를 계산할 때 $x_{\geq d}$의 입력이 0이 되도록 mask를 만들어 주면 된다.
가장 편한 방법은 binary mask matrix를 이용하는 것으로 0은 끊고 싶은 연결을 의미한다.
이를 위해 우리는 mask $M^W, M^V$를 정의하고, 적용해 autoregressive property를 유지한다.

여기서 mask $M^W, M^V$는 어떻게 정의할까?
우선 우리는 $m(k)$를 k번째 hidden unit에게 부여된 연결 가능한 최대값으로 정의한다.
$m(k)$는 1와 D-1 사이의 숫자로 할당한다.
0을 포함하지 않는 이유는 모든 connection이 다 끊긴 node를 만들 이유가 없기 때문이며, D를 포함하지 않는 이유는 모든 connection이 연결된 node를 만들 이유도 없기 때문이다.
mask $M^W, M^V$는 아래와 같이 정의된다.

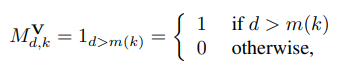
mask $M^W, M^V$는 일종의 connectivity를 나타낸다고 볼 수 있다. $M^{V, W} = M^VM^W$라고 정의하면 $M^{V, W}_{d', d}$는 input $x_d$와 output $\hat{x_d'}$의 connectivity를 나타낸다.
만약 $M^{V, W}$가 autoregressive property를 가지고 있다면, $M^{V, W}$는 strictly lower traingular matrix일 것이다. 이는 정의에 의해 쉽게 증명된다.
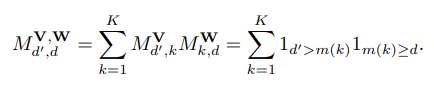
$d \geq d'$인 경우 $m(k)$보다 작거나 같은 $d$에 대해 $d'$이 $m(k)$보다 커야 하는데 $d$가 $d'$보다 크다 같으므로 $d'$은 $m(k)$보다 클 수 없다. 따라서 이 경우 모든 element는 0이다.
예시)

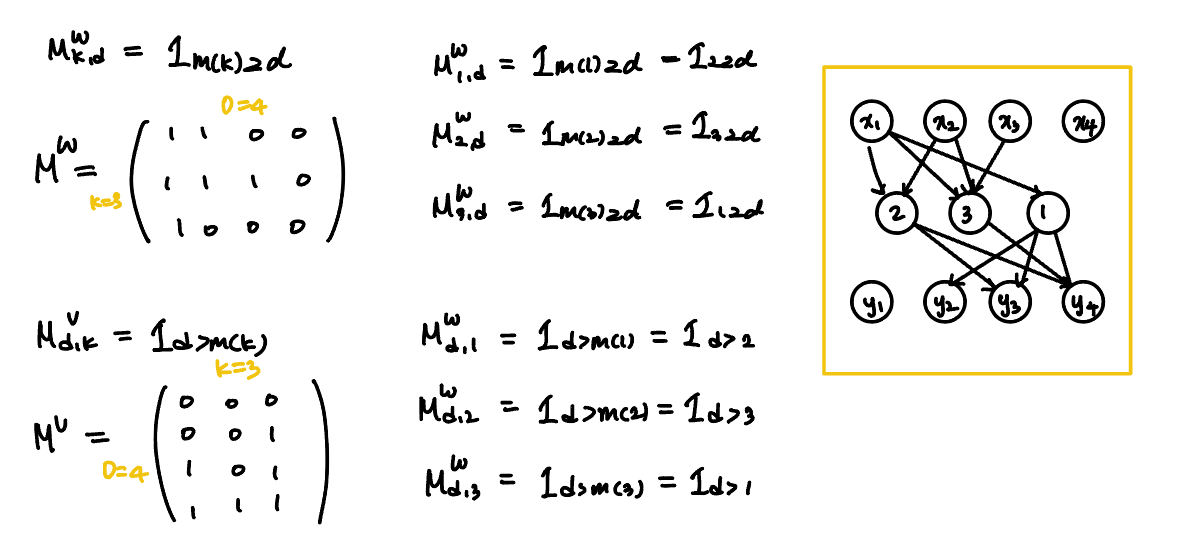
* 이 논문에서는 $m(k)$를 1와 D-1사이에서 uniform하게 sampling해서 사용했다.
* strictly lower triangular matrix A를 추가로 사용해 성능을 높였다.(과거 논문 참고)

Deep MADE
이제는 위에서 설명한 개념을 여러 개의 은닉 층와 은닉 유닛에 적용할 수 있도록 확장할 것이다.
L개의 은닉층이 있고, 각각의 은닉층의 matrix를 $W^i$이라고 하자. 각 은닉층의 은닉유닉을 $K^l$이라고 부르자. l번째 은닉층의 k번째 은닉층의 최대연결개수는 $m^l(k)$로 부르자.
여기서 첫번째 은닉층과 두번째 은닉층을 잇기 위해서는 아래와 같은 부등식을 만족해야 한다.

매우 중⭐요 예시)

따라서 mask $M^{W^l}, M^V$는 아래와 같이 정의된다.($M^V$는 은닉층에서 출력층으로 갈 때 쓰이므로 크게 변하지 않는다.)


* $m^l(k)$가 unconnect 유닛이 되는 것을 방지하기 위해 $m^l(k)$는 $min_{k'} m^{l-1}(k')$보다 크거나 같도록 샘플링된다.
예시)

Order-agnostic training
앞선 연구에서 autoregressive model을 학습할 때, 모든 순서에 대해 학습하는 것이 성능에 효과적이라는 논문이 있다고 한다. 그래서 MADE에서는 ordering을 랜덤하게 바꿔 학습한다.

이렇게 하므로써 일종의 ensemble(앙상블)을 만들어 학습시킨다고 볼 수 있다.
Connectivity-agnostic training
MADE에서는 order-agnostic training과 더불어 은닉층의 connectivity를 나타내는 $m^l(k)$를 바꾸므로서 agnoistic하게 학습할 수 있다. 그렇게 하기 위해 $m^l(k)$를 학습 전에 결정하기보다는, 각 배치마다 혹은 각 학습마다 $m^l(k)$를 만들어 학습하고자 한다.
이 과정은 그렇게 시간이 오래 걸리는 작업이 아니라는 점에 주목하자. 우리는 여기서 mask를 만드는 작업을 parallel하게 할 수 있다. $m^l = [m^l(1), ..., m^l(K^l)]$이라 두면, $M^{W^l}$을 쉽게 계산할 수 있다.(elementwise하게 1_{a \geq b}$ 연산을 수행하면 된다.)
$m^l(k)$를 계속 resampling할 때 문제점이 하나 있는데, 그것은 바로 connection이 없는 것과 0 unit을 neural net이 구분할 수 없다는 점이다.
이런 문제를 타계하기 위해 선행 연구에서는 각 은닉 유닛에게 입력을 제공하는 유닉을 알려주기 위해 binary indicator variable을 학습 가능한 추가적인 가중치로 사용한다. 이 논문에서도 비슷한 방법을 이용해 companion weight matrix $U^l$을 사용하고자 한다.

이러한 connectivity conditioning weights는 종종 유용한데 우리는 이를 일종의 hyperparameter로 선호에 맞게 사용할 수 있도록 했다.
* MADE에서는 학습의 안정성을 위해 모든 종류의 mask 사용보다는 종류를 한정하여 mask를 사용했다.
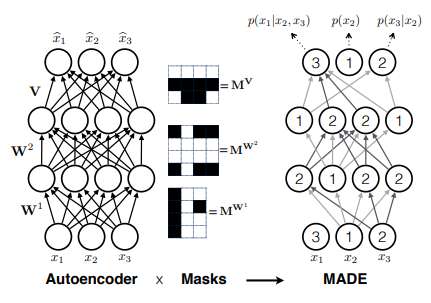
Pseudocode

☞ MADE는 neural net에서 autoregressive한 성질을 갖기 위해 mask를 정의해 density estimation을 진행했으며, 그 결과보다는 mask를 정의하는 방식이 많이 인용된다.
+ 구현 방법이 너무 간단해 소개한다!
출처 : pytorch_flows/flows_04.ipynb at master · acids-ircam/pytorch_flows · GitHub
class MaskedLinearAR(nn.Module): def __init__(self, in_dim, out_dim): super(MaskedLinearAR, self).__init__() self.in_dim = in_dim self.out_dim =out_dim self.weight = nn.Parameter(torch.Tensor(in_dim, out_dim)) self.bias = nn.Parameter(torch.Tensor(out_dim)) self.init_parameters() def init_parameters(self, ): nn.init.xavier_normal_(self.weight.data) self.bias.data.uniform_(-1, 1) def forward(self, input): output = input @ self.weight.tril(-1) output += self.bias return output'논문 리뷰 > Generative Model' 카테고리의 다른 글