-
cs236 5-6장 Latent Variable Models(VAEs)PROGRAMMING/머신러닝 2024. 6. 20. 20:55
Generative model 복습을 위해 CS236 강의를 듣고 정리해보고자 한다.
피피티는 아래 페이지를 참고하면 된다.
https://deepgenerativemodels.github.io/
※ PPT의 내용 정리와 더불어 같이 보면 좋을 자료들을 정리했습니다. 강의를 보고 이해한대로 작성했기 때문에 부정확한 내용이 포함되어 있을 수 있음을 알려드립니다. 또한 참고한 모든 블로그와 유튜브는 출처(Reference)에 있습니다.

미리 보는 정리본 Latent Variable Models : Motivation
사람의 얼굴을 생각해보자. 눈의 색깔, 머리의 색깔, 포즈, 성별 등등 다양한 factor들로 사람의 얼굴을 결정할 수 있다. 이때의 다양한 팩터들을 사람이 직접 정하지 않고 latent variable로 나타내보고자 한다. 만약 사람의 얼굴(=$x$)를 latent variable $z$를 통해 잘 정의한다면 $p(x)$보다 $p(x|z)$가 훨씬 간단할 것이다.

그렇다면 $z$가 Gaussian distribution을 따른다고 생각하고, $z$의 sample을 뽑는건 어떨까? 무수히 많은 $z$의 샘플은 하나의 factor에 대한 다양한 variation을 보여준다. $z$의 샘플 값은 사람의 얼굴 중 하나의 특성을 결정한다고 생각할 수 있으며, 우리는 학습 후 $z$가 의미있는 latent factors of variation이 되기를 바란다.

Mixture of Gaussian
복잡한 분포일지라도 가우시안 분포의 합으로 근사할 수 있다.
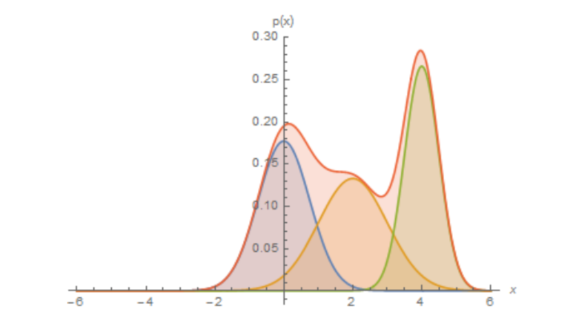
빨간색 분포 = 파란색, 노란색, 초록색 분포의 합으로 근사가 가능하다 즉, $p(x)$ 역시 K개의 gaussian 분포의 합으로 근사할 수 있을 것으로 예상 가능하다는 것이다.
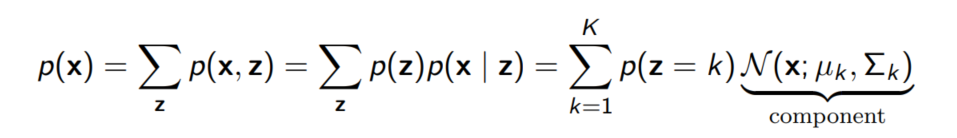
우리는 Mixture of Gaussian을 통해 Clustering과 Unsupervised learning을 할 수 있다.
Maximum Likelihood learning
joint distribution $p(X, Z; \theta)$을 생각하자. 데이터 셋 $D$에 대해 $X$ 변수는 관찰 가능하지만, $Z$ 변수는 관찰이 불가능하다. 그렇다면 데이터 셋 $D$의 M개의 샘플들 ${x^{(1)}, ..., x^{(M)}}에 대해 Maximum likelihood는 아래와 같이 쓸 수 있다.
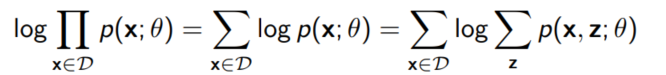
여기서 우리의 문제는 $ \log \sum_z p(x, z; \theta)$를 계산하기가 까다롭다는 점이다. z가 가능한 가짓수가 많아지면 많아질수록 z를 이용해 likelihood를 최대화 하는 것은 불가능하다.($Z$가 연속적인 확률 변수일 경우 더더욱 어렵다!!)
그렇기 때문에 우리는 Naive Monte Carlo를 먼저 생각해보고, Importance Sampling으로 좀 더 likelihood maximization을 발전시켜 볼 예정이다.
Naive Monte Carlo
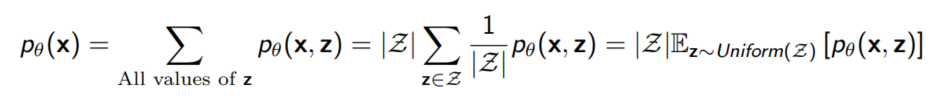
$\sum_z p(x, z; \theta)$를 평균으로 계산할 수 있도록 식을 변형해보았다. Monte Carlo Simulation을 이용하면 unbiased된 값을 얻을 수 있다는 점에서 좋지만, 실제로 위와 같은 방식은 잘 작동하지 않는다. 특히 $z$를 unifrom sampling하기 때문에 확률이 높은 부분에서 샘플링을 하는 것보다 의미있는 데이터를 생성할 z를 맞출 확률이 낮다.
그래서 우리는 importance sampling을 이용해 $z$를 uniform distribution이 아닌 다른 분포로 샘플링하는 아이디어를 생각해보았다.(=Importance Sampling)
더보기질문 1. $p_\theta(x, z)$를 계산한다는건 어떤 뜻일까?
Importance Sampling
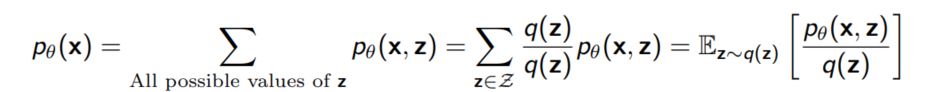
이번에는 확률분포 $q$를 importance sampling에 활용해보자. 직관적으로 $q$는 주어진 x에 대해 $p_{\theta}(x, z)를 고르는 것이 가장 좋은 선택일 것이다.
⭐ Importance Sampling에 대한 자세한 설명은 ↓ 참고 ⭐
Importance Sampling(중요도 샘플링)
Importance Sampling은 Monte Carlo Simulation을 할 때 variance를 줄여주는 중요한 테크닉 중 하나다.Importance Sampling을 ELBO를 증명하는데도 사용하길래 간단하게 정리해보았다.Importance SamplingImportance sampling은
jjo-mathstory.tistory.com
이렇게 구한 estimator 역시 $p_\theta (x)$의 unbiased estimator이다.
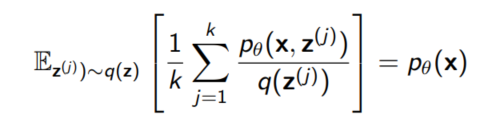
Estimating log-likelihoods
여기서 중요한 점은 우리가 필요한 것은 log-likelihood라는 점인데, log를 양변에 씌우는 순간 우리가 위에서 구한 estimator는 좋은 estimator가 되지 못한다. log 함수가 볼록 함수이기 때문이다!!
 더보기
더보기질문 1. 왜 오른쪽 식 그대로 계산하면 안될까?
log함수의 볼록성을 이용할 수 있는 부등식이 하나 있는데, 그건 바로 젠센 부등식이다.
Jensen's Inequality
If X is a random variable and $\pi$ is a convex function, then $\pi(E[X]) \leq E[\pi(X)] $
젠센 부등식에 의해 아래와 같이 식을 변형할 수 있다.(log를 Expectation 안으로 집어 넣을 수 있게 된다)

Evidence Lower Bound(ELBO)
$f(z) = \frac{p_\theta(x, z)}{q(z)}$라 두면 아래와 같이 구할 수 있고, 왼쪽에 있는 term을 Evidence Lower Bound, 줄여서 ELBO라 부른다.
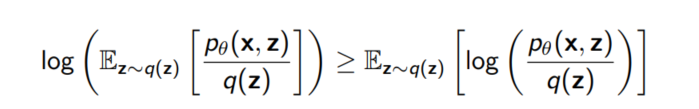
이번에는 특정 $q(z)$가 아닌 임의의 $q(z)$에 대해 생각해보자. 위 식을 바꿔쓰면 아래와 같이 전개가 가능하다.
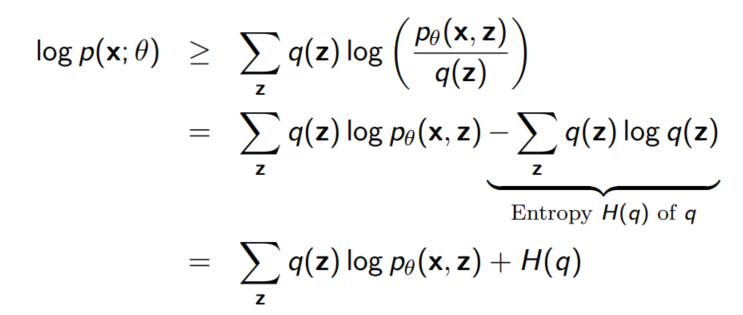
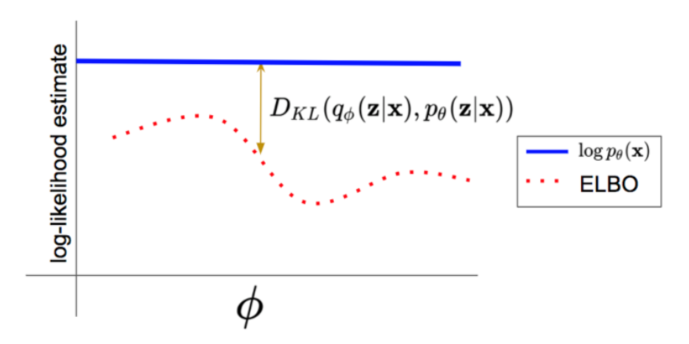
위 식의 등호는 $q$가 $p(z|x; \theta)$일 때만 성립한다.
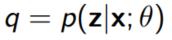
또한 $q = p(z|x; \theta)$이면 $D_{KL}(q(z) || p(z|x; \theta))$역시 0이 된다.(KL divergence의 정의에 비추어 봤을 때 당연한 말)

즉, 우측 term이 0이 되므로 우리는 아래 등호가 성립함을 알 수 있다.
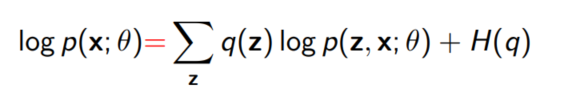
이 식은 ELBO + $D_{KL}(q(z)❘❘p(z❘x;\theta)$로도 쓸 수 있다. 이것은 우리가 처음 Importance Sampling을 도입했을 때의 직관과 일맥상 통한다. 처음에 우리는 $q$를 posterior distribution인 $p(z|x; \theta)$와 가장 가까운 확률분포로 정의하므로써 의미 있는 z의 샘플을 생성하기를 바랬었는데, 실제로 식에서도 이를 증명할 수 있다.
+위 계산 과정은 EM algorithm(Expectation-Maximazation)에서 E-step을 계산한 것과 동일하다.
★ EM 알고리즘 ★
EM 알고리즘 : 주어진 데이터에서 최대우도나 최대사후확률 추정을 찾는데 사용되는 방법론
E-step : 주어진 현재 추정치를 바탕으로 데이터의 'comple data log-likelihood'에 대한 기댓값을 계산한다. 여기서 'complete data'란 관측되지 않은 데이터(잠재 변수 또는 숨겨진 데이터 포함)까지 모두 포함된 데이터를 의미한다.
M-step : E-step에서 계산된 기대값을 최대화하는 새로운 파라미터 추정값을 계산한다.
EM 알고리즘에서는 E-step과 M-step을 수렴할 때까지 반복한다.
Intractable Posteriors
만약 $p(z|x; \theta)$가 intracatable하다면 어떻게 해야할까?
VAE에서는 $p(z|x; \theta)$를 $p(x|z)$의 역변환으로 생각하는데, 여기서 $\mu_{\theta}$와 ${\Sigma_{\theta}$는 neural networks이다.
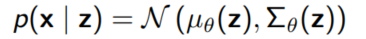
만약 $q(z; \phi)$가 $\phi$에 의해 결정되는 hidden layer의 tractable한 확률분포라고 하자.
예를 들어 $q(z; \phi)$가 $\phi$에 의해 결정되는 정규분포일 때를 생각해보자.
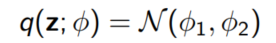
우리는 $\phi$를 잘 골라 $q(z; \phi)$가 $p(z|x; \theta)$와 가깝기를 바란다.

그림에서 파란색 $p(z|x; \theta)$에 가까운 정규분포는 초록색과 주황색 중 주황색 정규분포이다. 따라서 우리는 $\phi$를 잘 조정해서 주황색 정규분포를 고를 수 있도록 하는 것이다.
더보기※ 참고
$\phi$는 $q(z)$를 결정하는 parameter이다. 앞에서는 고려하지 않은 $\phi$를 조정해 $q(z, \phi)$를 조정할 수 있다.
우리의 부등식은 $\phi$를 사용해 다시 쓸 수 있다.
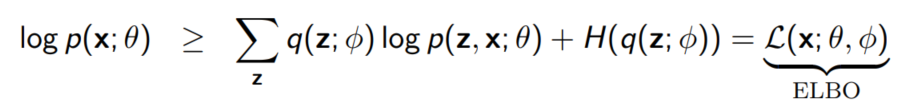

사실상 우리는 $\theta$와 $\phi$를 모두 학습시켜야 한다는 결론에 이른다.

ELBO를 전체 데이터셋에 대해 나타나면 다음과 같이 나타낼 수 있다.
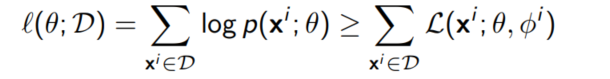
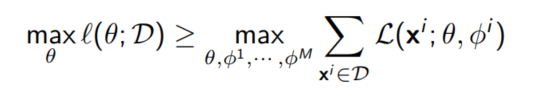
여기서 각각의 데이터 포인트 $x^i$에 대해 서로 다른 파라미터 $\phi^i$를 선택했다는 사실을 눈여겨 볼 필요가 있다. true posterior $p(z|x^i;\theta)는 데이터 포인트 $x^i$에 따라 달라지기 때문이다.
Stochastic Variational Inference(SVI)
전체 데이터 셋에 대한 ELBO를 학습시키기 위해서는 $\theta, \phi^1, ..., \phi^M$에 대해 gradient descent를 수행해야 한다.
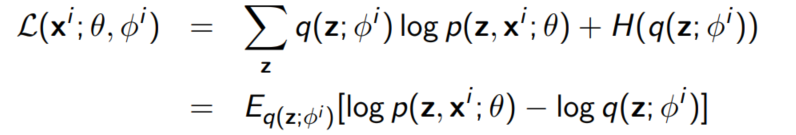
다음은 stochastic gradient descent를 수행하는 알고리즘이다.

여기서 gradient를 구하기 위해 Monte Carlo sampling을 수행할 예정이다.
$q(z; \phi)$에서 $z^1, ..., z^K$를 뽑아 아래와 같이 추정한다.

$\phi^i$에서 $i$는 생략 여기서의 가정은 $q(z; \phi)$는 tractable하기 때문에 샘플을 만들고 값을 계산하는 것이 쉽다는 점이다.

Goal!!!! Gradient with respect to $\theta$
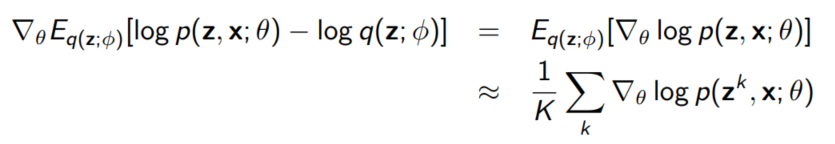
Gradient with respect to $\phi$ - more complicative
$q(z; \phi) = N(\mu, \sigma^2I)$ with $\phi = (\mu, \sigma)$라고 가정하자.
$z \sim q(z; \phi)$에서 샘플링 하는 것은 $\epsilon \sim N(0, I)$에서 샘플링하고 $z = \mu + \sigma \epsilon = g(\epsilon; \phi)$하는 것과 동일하다.

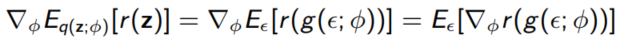
이러한 technique를 Reparameterization이라고 부른다 위와 같은 성질은 z가 continuous하고, r과 g가 $\phi$와 $\epsilon$에 대해 미분 가능할 때 쉽게 계산된다.
Monte Carlo Sampling을 이용하면 아래와 같이 표현 가능하다.
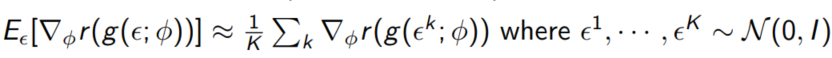
다시 ELBO로 돌아가보자.
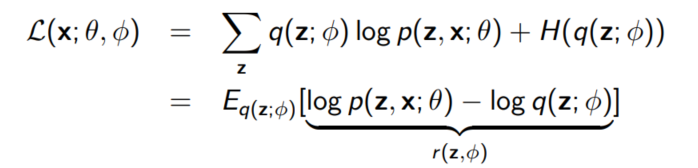
$z = \mu + \sigma \epsilon = g(\epsilon; \phi)$로 reparameterization해보자.
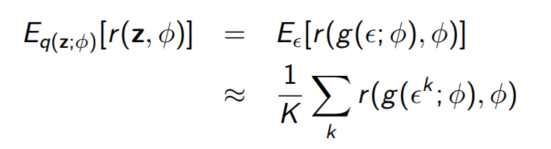
위와 같이 식이 나오므로 chain rule을 사용하면 어렵지 않게 gradient를 구할 수 있다.
Amortized Inference
지금까지는 각각의 데이터 셋에 대해 variational parameters $\phi$를 대응시켜 생각했다. 이제는 single parametric functoin $f_{\lambda}$를 생각해보자.
즉, 원래는 각각의 $x^i$에 대해 ${\phi}^i$를 생각했다면 이제는 각각의 $x^i$에 대해 ${\phi}^i$로 보내는 하나의 매핑을 생각하는 것이다.
Goal : posteriors $q(z|x^i)$를 $q_{\lambda}(z|x)$로 근사
$p(z, x^i; \theta)$가 $p_{data}(z, x^i)$와 근사하다고 가정하자. 또한 $q(z; {\phi}^i)$가 hidden variables z에 대해 tractable probability distribution이라고 하자.

* 이 강의에서는 $q(z; f_{lambda}(x^i))$를 $q(z; f_{\phi}(z|x))$로 쓴다.
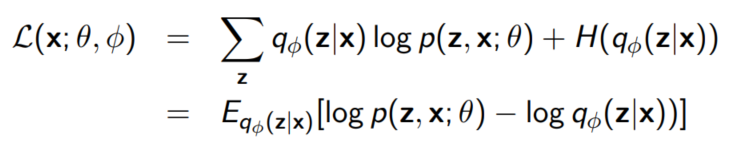
위 식을 학습하기 위해서는 아래와 같은 과정을 반복한다.

gradient를 계산하기 위해서는 위와 마찬가지로 reparameterization 방법을 사용한다. Autoencoder perspective

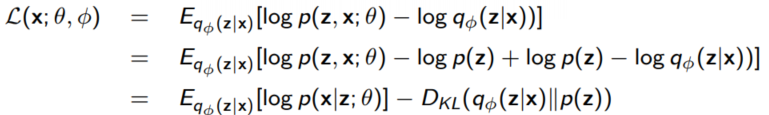
Autoencoder view에서 다음과 같이 encode하는 과정과 decode하는 과정 2개로 나눠 생각해볼 수 있다.
1. data point $x^i$를 뽑아 이를 $q_{\phi}(z|x^i)$에서 뽑은 $\hat{z}$로 매핑한다.
2. $\hat{x}$를 복원하기 위해 $p(x|\hat{z}; \theta)$에서부터 샘플링한다.
연구발전 방향은 아래와 같다. 1, 2, 3번의 과정을 발전시키는 과정으로 연구가 진행되어 왔다.
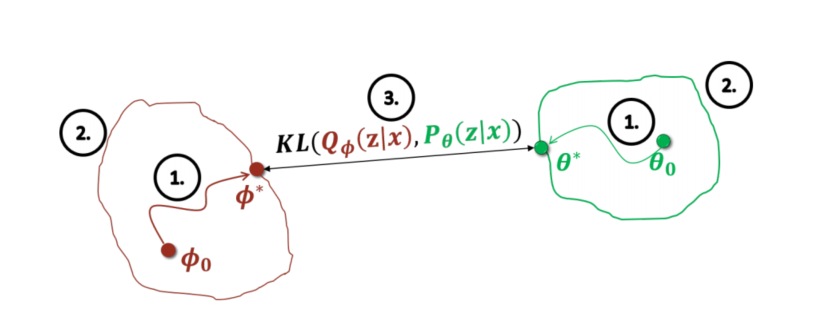
Reference
[1] cs236 5, 6장 강의
[2] https://norman3.github.io/prml/docs/chapter09/4.html
4. The EM Algorithm in General
\( EM \) : Expectation Maximization Algorithm
norman3.github.io
[3] https://www.quora.com/unanswered/What-is-amortized-variational-inference
What is amortized variational inference?
6 people want answers to this question. Be the first to answer.
www.quora.com
[4] https://ricoshin.tistory.com/3
Amortized Inference란?
https://www.quora.com/What-is-amortized-variational-inference What is amortized variational inference? Answer: Let me briefly describe the setting first, as the best way to understand amortized variational inference (in my opinion) is in the context of reg
ricoshin.tistory.com
'PROGRAMMING > 머신러닝' 카테고리의 다른 글
Importance Sampling(중요도 샘플링) (0) 2024.06.19 CS236 4장 Maximum Likelihood Learning (0) 2024.06.14 CS236 3장 Autoregressive Models 정리 (2) 2024.06.12