-
EDM 논문 리뷰(Elucidating the Design Space of Diffusion-Based Generative Models)논문 리뷰/Generative Model 2024. 8. 29. 13:31
Diffusion model을 실용적으로 발전시킨 논문. 근데 말도 너무 어렵고, 내용도 어려워서 많은 이 세상 고수님들의 도움을 받았다. 크게 도움을 받은게 바로 이 유튜브 강의!!! 이상윤님이 발표하신 강의인데, notion 정리본까지 주셔서 감사할 따름니다...
EDM 이해에 어려움을 겪는 모든 분들에게 강추합니다🔥
유튜브 강의 : https://www.youtube.com/watch?v=FSSAieHkX88
(노션 링크는 유튜브 페이지에서 바로 눌러야 유효한거 같기도 합니닷...!)
Elucidating the Design Space of Diffusion-Based Generative Models | Notion
Motivation
sang-yun-lee.notion.site
Introduction
이 논문에서는 기존의 diffusion model들이 on a solid theoretical footing이라고 지적하며, 다양한 분석 방식을 통해 design space를 발전시킨다. 이 논문은 샘플링 과정에서
(1) the best-performing time discretization
(2) apply a higher order Runge-Kutta method
(3) evaluate different sampler schedules
(4) analyze the usefulness of stochasticity를 연구한다.
또한 네트워크의 input, output, loss function의 preconditioning(전처리), 학습 중 noise level의 분포에 대해 제안하며 GAN에서 자주 쓰이는 non-leaking augmentation을 활용한다. 이와 같은 연구를 통해 edm은 기존의 모델 성능을 획기적으로 끌어올린다.
* design space : 시스템이나 모델을 설계할 때 가능한 모든 선택지와 구성을 포함하는 개념적 공간(네트워크 아키텍쳐, 알고리즘, 샘플링 방법, 전처리/후처리 등)
Expressing diffusion models in a common framework
데이터 분포 pdata(x), 표준편차 σdata에 대해 i.i.d. 가우시안 노이즈를 추가하여 얻어진 mollified distributions p(x;σ)를 생각해보자. σmax가 σdata보다 훨씬 큰 경우, p(x;σmax는 순수한 가우시안 노이즈와 거의 비슷하다. 확산 모델은 노이즈 이미지 x0∼N(0,σ2maxI)를 무작위로 샘플링한 다음, 노이즈 수준 σ0=σmax>...>σN=0인 이미지 xi로 순차적으로 디노이징한다.
※ 이 논문에서는 x0를 순수한 노이즈로, xN을 이미지로 보고 있다.
이 과정은 Song에 의해 SDE로 표현되며, Probability flow ODE(PF ODE)로도 표현가능하다. 일반적으로 많은 논문들은 SDE를 먼저 소개하나, EDM에서는 ODE approach를 먼저 설명하고 있다.
ODE formulation & Denoising score matching
노이즈 스케줄 σ(t)는 많은 경우 √t와 비례해서 세팅하는 것이 수학적으로 자연스러우며, constant-speed heat diffusion과 대응된다. 하지만 노이즈 스케줄이 성능과 연관이 깊기 때문에 이에 대한 고찰이 필요하다. 일반적으로 PF ODE는 아래 식과 같이 나타난다.

D(x;σ)는 denoiser function으로 각 σ에 대해 pdata에서 추출된 샘플의 expected L2 denoising error를 최소화한다면, 스코어 함수는 아래와 같이 표현될 수 있다.(y는 training image, n은 noise)

D(x;σ)는 Dθ(x;σ)로 구현될 수 있으며, 전처리 및 후처리 단계가 포함될 수 있다. 아래 그림은 이상적인 D의 동작을 보여준다.

Time-dependent signal scaling & Solution by discretization
스케일 스케줄 s(t)를 도입하여 x=s(t)ˆx으로 생각해보자. 그러면 아래와 같은 ODE를 얻을 수 있다.(앞에서 얻은 PF ODE의 일반화된 버전)

참고로 score function을 평가할 때는 p(x;σ)의 정의가 s(t)와 독립적이도록 하기 위해 x의 스케일링을 명시적으로 해제한다.
이제 앞에서 제시한 D 관련 식을 바로 위 식에 대입하여 numerical integration을 통해 해를 찾으면된다. 일반적으로는 Euler method를 많이 사용하지만, EDM에서는 2nd order solver를 사용해 성능을 끌어올린다.

Improvements to deterministic sampling
이 논문에서는 샘플링 과정을 어떻게 설정할 것인지는 다른 네트워크 아키텍쳐나 학습 디테일과는 독립적이라는 가정을 깔고 실험을 진행한다. 즉, Dθ를 학습하는 과정이 σ(t),s(t),{ti}를 결정해는 안된다는 점이다. 이러한 관점에서 Dθ는 그저 black-box로 간주되어야 한다. (그리고 이 가정은 샘플링 프로세스를 발견시킴에 따라 지속적으로 성능이 발전하는 아래 실험에서 입증되었다고 볼 수 있다.)
EDM에서는 다양한 sampler를 세 개의 pre-trained model(DDPM++ cont, NCSN++ cont, ADM(dropout))을 이용해 실험해보았다. (실험 관련 내용은 Appendix C에서 확인 가능) 그 결과는 FID로 나타냈으며, 아래 그림은 FID를 NFE(neural function evaluation)의 함수로 나타내었다. NFE는 하나의 이미지를 생성하는데 Dθ를 몇 번 계산해야 하는지를 타나낸다. 샘플링 과정에서 Dθ의 비용이 큰 비중을 차지하고 있기 때문에 적은 NFE로 좋은 FID 점수를 얻을수록 샘플 생성 속도가 빠르다고 할 수 있다.

파란색 선은 원래의 샘플러를 이용한 것이고, 주황색 선은 구현에서 간과된 몇가지 부분과 이산화 노이즈 수준을 더 신중하게 처리한 결과를 나타낸다. 초록색 선은 Heun's method를 적용한 것이다. 빨간색 선은 σ(t)=t, s(t)=1로 설정했을 때의 모습이며, 가장 좋은 퍼포먼스를 보여준다. DDIM의 경우 기존 모형이 σ(t)=t, s(t)=1으로 설정하였으므로, 초록색 선과 빨간색 선이 동일한 결과를 나타냄을 알 수 있다. 검은색 선은 RK45 method를 ODE solver로 사용한 결과로 더 정교한 ODE solver를 사용했음에도 괄목할만한큼 뛰어난 결과를 보여주지는 못한다.
original 샘플러들은 Euler's method를 사용해 ODE를 numerical하게 풀었는데, Euler's method는 1차 ODE 솔버로 step size가 h일 때, O(h2)의 local error를 가지고 있다. Higher-order Runge-Kutta methods가 더 좋은 FID를 가져올 수 있지만, 이는 Dθ의 계산량을 늘린다. EDM에서는 Heun's 2nd order method(a.k.a. improved Euler, trapezoidal rule)을 사용해 truncation error와 NFE 사이의 균형을 잡는다. 아래 알고리즘에서 6, 7, 8번 라인이 Euler's method에서 추가된 것으로 xi+1에 대한 추가적인 correction step을 거쳐 ti와 t_i+1} 사이에 dx/dt의 변화를 보정한다. 이 보정 단계는 O(h3)의 local error를 초래하며, 각 단계에서 Dθ를 한 번 더 평가하게끔 한다. σ=0인 경우 0으로 나누는 경우가 발생하지 않게끔 이 경우에만 Euler's method를 사용한다.

time step {ti}에 대해 step size는 σ가 감소함에 따라 단조감소해야 하며, 샘플별로 다를 필요가 없음을 Appendix D에서 자세한 설명과 함께 주장한다. 따라서 EDM에서는 시간 단계를 {σi}에 따라 ti=σ−1(sigmai)로 정의한다. 여기서 σi<N=(Ai+B)ρ로 설정하고 A=(σ1ρmin−σ1ρmax)/(N−1), B=σ1ρmax로 설정하여 σ0=σmax, σN−1=σmin이 되도록 한다.

여기서 ρ는 시간 단계가 노이즈 수준 σ에 따라 어떻게 분포되는지를 제어하는 매개변수다. ρ가 클수록 σmin 근처에서는 시간 단계가 더 작아지고, σmax 근처에서는 시간 단계가 더 길어진다. 즉, ρ가 크면 클수록 작은 노이즈 수준에서는 더 세밀한 변화를, 큰 노이즈 수준에서는 더 큰 변화를 유도하게 된다.
ρ=3로 설정하면 각 단계에서 truncation error가 거의 동일하지만, ρ가 5에서 10 사이일 때 이미지 샘플링 성능이 훨씬 좋다. 이는 σmin 근처의 오류가 큰 영향을 미친다는 것을 시사한다. 이 논문에서는 ρ=7로 설정한다.
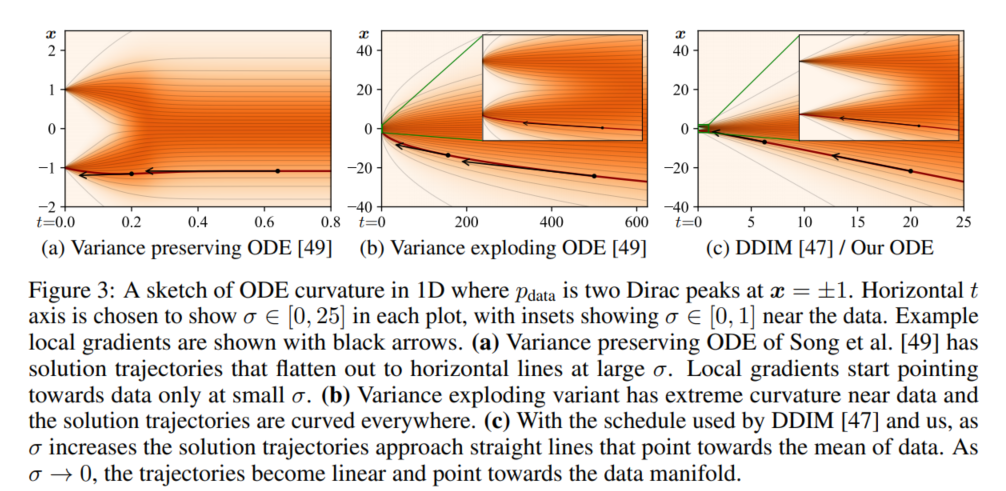
앞에서 ODE는 σ(t)와 s(t)에 의해 정의된다. 이 논문에서는 σ(t)=t, s(t)=1로 설정함으로서 truncation error를 최소화할 수 있을 것이라고 주장하는데(이러한 σ(t)와 s(t)의 설정은 DDIM과 동일), 그 이유는 trucation error의 크기가 dx/dt의 곡률에 비례하기 때문이다. 위와 같이 σ(t)와 s(t)를 설정하면 ODE는 dx/dt=(x−D(x;t))/t로 간단하게 바뀌며, σ와 t는 interchangeable해진다. 즉, σ(t)=t이;므로 샘플링 과정에서 시간 변수를 사용하는 것은 노이즈 변수를 사용하는 것과 동일한 효과를 가져온다.
위 식에서 solution tragectory의 접선은 항상 Denoiser D의 출력 방향을 가리키게 된다. 이 변화는 노이즈 수준에 따라 천천히 진행될 것이며, 대체로 선형적인 모양을 한다. 해 궤적은 큰 노이즈와 작은 노이즈 수준에서는 선형에 가까우며, 중간 영역에서만 상당한 곡률을 가진다. 즉, Denoising이 주로 특정 σ의 범위 내에서 이루어지며, 이 범위 밖에서는 큰 변화가 일어나지 않는다는 것이다. 따라서 변화가 많이 일어나는 σ의 범위를 잘 활용하여 그 구간에서 Denoiser가 효과적으로 작동할 수 있도록 스케줄을 설계하는 것이 중요하다.
Stochastic sampling
ODE를 활용한 Deterministic sampling은 노이즈를 추가하지 않고도 이미지를 생성하는 방법으로 생성된 이미지를 역으로 계산해 latent representation을 얻을 수 있다는 점이다. 이론적으로는 Deterministic sampling과 Stochastic sampling이 동일한 분포를 recover할 수 있다고 알려져 있으나, 실제로는 Stochastic sampling의 성능이 더 좋다.
그러다면 stochasticity의 역할은 정확히 무엇일까?
Song이 제안한 SDE는 아래와 같이 일반화되어 PF ODE와 Langevin diffusion SDE의 합으로 나타낼 수 있다.

여기서 β(t)는 기존 노이즈가 새로운 노이즈로 대체되는 상대적인 비율을 나타낸다.
implicit Langevin diffusion은 샘플이 원하는 marginal distribution이 될 수 있도록 유도하면서, 이전 샘플링 단계에서 발생한 오류를 교정한다. 하지만 Langevin항을 discrete SDE solver로 근사하면 오류가 발생하기 마련이다. 따라서 어떤 β(t)를 고를지는 실험을 통해 정해야 한다. 참고로 Song은 β(t)=˙σ(t)σ(t)로 설정하여 forward SDE가 사라지게 했다. (다만 이 β(t)는 큰 의미는 없어보인다.)
Suggested stochastic sampler
'We propose a stochastic sampler that combines our 2nd order deterministic ODE integrator with explicit Langevin-like "churn" of adding and removing noise.'
이 논문에서 제안한 확률적 샘플러는 아래 알고리즘 2에서 제안되고 있다.

이 알고리즘은 샘플에 γi에 따라 노이즈를 추가하여 더 높은 노이즈 수준 ^ti=ti+γiti로 도달하게 한다. 그 다음 증가된 노이즈 샘플 ^xi에서 ^ti에서 ti+1로 ODE를 역방향으로 한 단계만 수행하여 샘플 xi+1을 얻는다. 이 과정은 이미지를 얻을 때까지 지속한다.
이 샘플러는 일반적인 SDE solver는 아니며, Song이 제안한 predictor-corrector 샘플러와 유사한 구조를 가진다. Euler-Maruyama(EM) 방법과의 차이점을 살펴보면, EM은 먼저 노이즈는 추가한 채, x와 σ는 그대로 있다고 가정하고 한 스텝 진행하는데 비해, 이 방법은 7번째 줄에서 Dθ를 평가할 때 사용되는 매개변수들이 노이즈 주입 후의 상태( ^xi, ^ti )에 해당한다. step size가 작아지면 이 둘은 차이가 없지만 낮은 NFE와 큰 스텝 사이즈에서는 성능에 큰 차이를 보인다.
stochasticity의 양을 늘리는 것은 이전 샘플링 단계에서 발생한 오류를 수정하는데 효과적이지만, 모든 데이터셋과 Denoiser 네트워크에서 생성된 이미지의 세부 사항이 점진적으로 손실되는 결과를 초래한다. 저자들은 Denoiser가 slightly non-conservative vector field를 유도하여 이러한 결과를 초래한다는 가설을 세운다.
* conservative vector field : 경로에 무관하게 시작점과 끝점 사이의 일만 고려하는 vector field
* non-conservative vector field : 경로에 따라 결과가 달라질 수 있는 vector field로 디노이저가 이미지의 노이즈를 제거하는 과정에서 경로에 따라 일관성 없이 작동할 수 있음을 의미
만약 Dθ(x;σ)의 결함으로 문제가 발생한 것이라면 샘플링 과정에서의 문제는 heuristic하게 해결할 수 밖에 없다. 이 논문에서는 oversaturated color를 방지하기 위해 특정 노이즈 수준 ti∈[Stmin,Stmax] 범위 내에서만 stochasticity를 허용한다. 이러한 노이즈 레벨에 대해 γi=Schrun/N으로 정의하며, Schrun은 overall amount of stochasticity로 정의한다. 또한 이미지에 이미 존재하는 노이즈보다 더 많은 새로운 노이즈가 도입되지 않도록 γi를 제한한다. 마지막으로, 세부사항의 손실을 부분적으로 상쇄하기 위해 Snoise를 1보다 약간 크게 설정하여 새로 추가된 노이즈의 표준편차를 증가시켰다. 이는 Dθ(x;σ)가 non-conservativity를 가지고 있어 과도하게 노이즈를 제거하는 경향이 있음 보여준다. 왜냐하면 Denoiser는 L2로 학습되어 평균으로 회귀하려는 성질을 가지 있기 때문이다.
아래 실험 결과에서 보이듯 EDM에서 제안한 Stochastic sampler는 다른 sampler보다 성능이 뛰어나며, 특히 low step counts에서 큰 차이를 보인다. 다만 최적의 결과를 얻기 위해서는 여러가지 heuristic한 결정을 해야한다는 단점이 있으며, 이 논문에서는 Schurn,Stmin,Stmax,Snoise의 최적 값을 찾기 위해 그리드 검색을 활용했다.

Preconditioning and training
기존에는 σ-dependent normalization factor를 사용해 Dθ(x;σ)=x−\sigmaFθ(˙)이라고 설정했으나, 네트워크가 만든 오류가 σ의 값에 따라 증폭된다는 단점이 있었다. 이를 극복하고자 이전 연구들에서 사용한 signal와 noise를 혼합하는 방식과 유사하 게 다음과 같은 형태의 Dθ를 제안한다.

또한 전체 loss function은 다음과 같이 제안된다.

여기서 ptrain(σ)은 특정 노이즈 수준 σ가 샘플링될 확률을 나타낸다. 위 손실함수를 Fθ로 나타내면 다음과 같다.

여기서 cin,cout은 입력과 훈련 목표가 unit variave를 가지도록, cskip은 네트워크의 오류를 최소화하도록, cnoise는 실험적으로 최적의 값으로 설정한다.
아래 실험은 deterministic sampler를 사용해 FID 값을 구한 것으로 (A) Song의 기본 훈련 구성에서 (B) 기본 하이퍼파라미터를 재조정하고, (C) 가장 낮은 해상도의 레이어를 제거 / 가장 높은 해상도의 레이버 용량 2배 높여 모델의 표현력을 증가시키고 (D) 원래의 {cin,cout,cskip,cnoise}를 논문 제시 방식으로 대체하였다. 특히 D는 FID 값 자체를 개선하지는 않았으나, 훈련을 더 견고하게 만들었다.

Fθ를 훈련할 때, 각 샘플의 손실 가중치는 λ(σ)cout(σ)2로 설정된다. λ(σ)=1cout(σ)2로 설정하면 전체 σ의 범위에서 초기 훈련 손실이 균등해진다.(아래 그림에서 초록선)
p\traini(σ)를 고르기 위해 훈련 후 각 σ별 손실을 분석한 결과, 중간 노이즈 수준에서만 손실을 크게 줄일 수 있음을 발견했다. 낮은 노이즈 수준에서는 노이즈 성분을 구별하기 어려웠으며, 높은 노이즈 수준에서는 훈련 목표가 데이터 셋의 평균과 비슷해지는 경향이 있다. 따라서 이 논문에소는 p\traini(σ)를 log-normal distribution으로 설정한다.

EDM에서는 GAN에서 많이 쓰이는 Augmentation Regularization을 도입하여 과적합을 막고자 한다. 방법은 훈련 이미지에 노이즈를 추가하기 전 다양한 기하학적 변환을 적용한다. 이 augmentation이 이미지 생성에 영향을 주는 것을 막기 위해 증강 매개변수를 Fθ에 조건 입력으로 제공한다. inference 중에는 이 매개변수를 0으로 설정해 augment되지 않은 이미지 생성을 보장한다. 이러한 Augmentation 방법은 FID 값을 매우 좋게 만든다.
흥미롭게도, 모델 자체의 성능이 개선됨에 따라 stochastic sampling의 중요성이 감소했다. 이는 위 그림 (b), (c)를 통해 알 수 있는데, EDM에서 제안한 방법을 모두 적용하면 deterministic sampling이 stochastic sampling보다 오히려 더 좋은 성능을 가져온다.
ImageNet-64 데이터셋의 경우, class-conditional model을 제안된 훈련 개선 사항들과 함께 학습하였으며, 새로운 최고성능 1.48 FID를 달성하였다. 여기서는 overfitting이 문제가 되진 않았으며, augmentation regularization도 사용하지 않았다. 이 모델은 적은 샘플링 만으로도 최상의 결과를 얻을 수 있었으며, stochastic sampling이 deterministic sampling보다 좋은 성능을 보여준다. 여기서 알 수 있듯이 더 다양한 데이터셋이 확률적 샘플링에서 이점을 얻을 수 있다.
Conclusion
Our approach of putting diffusion models to a common framework exposes a modular design. This allows a targeted investigation of individual components, potentialy helping to better cover the viable design space. In our tests this let us simply replace the samplers in various earlier models, drastically improving the results. For example, in ImageNet-64 our sampler turned an average model(FID 2.07) to a challenger(1.55) for the previous SOTA model(1.48), and with training improvements achieved SOTA FID of 1.36. We also obtained new state-of-the-art results on CIFAR-10 while using only 35 model evaluations, deterministic sampling, and a small network. The current high-resolution diffusion models rely either on separate super-resolution steps, subspace projection, very large networks, or hybrid approaches - we believe that our contributions are orthogonal to these extensions. That said, many of our parameter values may need to be re-adjusted for higher resolution datasets. Furthermore, we fell that the precise interaction between stochastic sampling and the training objective remains an interesting question for future work.
'논문 리뷰 > Generative Model' 카테고리의 다른 글
