Score-Based SDE(Score-Based Generative Modeling Though Stochastic Differential Equaitons) 논문 리뷰

Score-Based SDE 논문을 읽어보았다. 이 논문을 이해하기 위해서는 우선 SMLD와 DDPM에 대해 이해하고 있어야 한다. 

 

SMLD과 DDPM 정리 포스팅입니다

 

* SMLD(Score Matching with Langevin Dynamics)와 NCSN(Noise Conditional Score Network)의 차이점 :

NCSN은 SMLD 방법을 사용하여 훈련된 모델이다. SMLD는 스코어 기반 생성 모델로서 사용되는 방법론으로, 데이터의 변환을 위해 score matching과 Langevin Dynamics를 결합한다. 

 

이 논문의 메인이 되는 그림↓

Abstract

이 논문은 data distribution에서 known prior distribution으로 변환하는 SDE를 소개하고, reverse-time SDE를 통해 prior distribution을 data distribution으로 변환하는 방법을 소개한다. 여기서 reverse SDE는 time-dependent gradient field, 즉 score에만 의존한다. neural net을 통해 score를 추정하며, numerical SDE solver를 통해 sample을 생성한다. 또한 discretized reverse-time SDE과정에서 발생하는 오류를 수정하기 위해 predictor-corrector framework를 도입한다. 이 논문에서는 또한 probability flow ODE라는 SDE와 동일한 분포를 공유하는 ODE를 제안하므로서 정확한 likelihood 계산과 향상된 sampling 효율성을 제공한다. 

 

[ 부연 설명 ]

Diffusion 확률 모델(이하 DPM)과 앞서 살펴본 Score-based Generative Model(이하 score-based model)이 꽤 유사해보이는데, 데이터를 multiple scale noise로 perturb하고 denoise하는 방식으로 샘플을 얻는다는 공통점이 있다. 하지만 DPM은 ELBO를 사용하여 학습하고 학습된 decoder를 사용하여 샘플링하며 Score-based model은 score matching objective를 사용하여 학습, Langevin dynamics을 사용하여 샘플링한다는 차이가 있다.

 

후에 2020년에 나온 논문인 DDPM은 score-based model과 DPM의 깊은 연관성에 대해 연구하였는데 DPM을 학습하기 위해 사용하는 ELBO가 score-based model에서 사용하는 score matching objective의 가중치를 주고 조합한 것과 동일하다는 것을 밝혔다. decoder를 U-Net 아키텍처를 사용하여 score-based model의 sequence로 parameterize하여 DPM이 GAN의 샘플 퀄리티를 넘어서는 성과를 낼 수 있음을 보였다.

 

Yang Song(Score-based model 저자)는 DDPM에서 영감을 받아 DPM과 score-based model의 관계를 더 조사하였고 이를 담은 논문인 Score-Based Generative Modeling through Stochastic Differential Equations을 2021년에 제출하였다.

저자는 DPM의 샘플링 방식을 score-based model의 Annealed Langevin dynamic과 결합하여 통합된 강력한 sampler(the Predictor-Corrector sampler)를 만들 수 있음을 발견하였다. 또 noise scale의 총 개수를 무한으로 늘리면 DPM과 score-based model 모두 score function에 의해 정의되는 stochastic differential equations의 이산화로 볼 수 있다는 것을 증명하였고 score-based model과 DPM을 하나의 프레임워크로 연결하였다.

 

최신 연구들은 DPM과 score-based model이 동일한 model family의 다른 관점이라는 것을 밝히는데까지 성공하였다.

출처: https://dlaiml.tistory.com/entry/Score-based-Generative-Models과-Diffusion-Probabilistic-Models과의-관계 [Deeper Learning:티스토리]

 

Introduction

앞에서 한 설명들

만약 noise를 연속적으로 주입하는 diffusion process를 상정하면, forward process는 data에 의존하지 않고, 이미 정해진 SDE로 나타날 수 있다. reverse-time SDE는 forward SDE와 marginal probability density의 gradient인 score로 나타난다. 우리는 reverse-time SDE를 neural network로 근사하여 numerical SDE solver를 통해 샘플을 생성할 수 있다. 그리고 이 과정을 아래 그림으로 요약할 수 있다.

 

장점

1. 유연한 샘플링 및 likelihood 계산 : 어떤 SDE solver든 reverse-time SDE 샘플링을 위해 사용할 수 있다. 이 논문에서는 i) Predictor-Corrector(PC) sampler와 ii) deterministic samplers based on the probability flow ODE를 제안한다. PC sampler는 numerical SDE solver를 score-based MCMC 방법론과 함께 사용하며, PF ODE sampler의 경우 ODE solver 기반이므로 빠른 샘플링이 가능하며, flexible data manipulation via latent codes, a uniquely identifiable encoding, exact likelihood computation이 가능하다.
2. generation의 controllable : 훈련시 사용하지 않은 정보에 조건을 부여하여 생성 과정을 조정할 수 있다. (class-conditional generation, image inpainting, colorization 등등)
3. 통합된 framework : SMLD와 DDPM 방법론은 각각의 SDE를 이산화한 것으로 이 framework에 통합될 수 있다.

Background

Denoising Score Matching With Langevin Dynamics(SMLD)

 

Denoising Diffusion Probabilistic Models(DDPM)

 

Score-Based Generative Modeling with SDEs

앞서 소개한 SMLD와 DDPM의 방법을 일반화시켜 무한한 수의 노이즈 스케일로 확장해보자.

 

우리의 목표는 diffusion process $ \{ x(t) \}_{t=0}^{T}$, $ t \in [0, T]$, $x(0) \sim p_0$를 만드는 것이다. 여기서 $p_0$는 data distribution이며, $p_T$는 prior distribution이다. 이러한 diffusion process는 아래와 같은 SDE로 나타낼 수 있다. 

여기서 $ f(\cdot, t) : \mathbb{R}^d \rightarrow \mathbb{R}^d $는 drift coefficient of $x(t)$, $ g(\cdot) : \mathbb{R} \rightarrow \mathbb{R} $는 diffusion coefficient이다. 이 SDE는 coefficients가 globally Lipschitz in both state and time인 경우 unique strong solution를 갖는다. 여기서 $p_t(x)$는 $x(t)$의 probaiblity density, $p_{st}(x(t)|x(s))$는 $x(s)$에서 $x(t)$로의 transition kernel form이라고 두자. 

 

일반적으로 $p_T$는 $p_0$에 대한 정보가 없는 unstructured prior distribution이며, 평균과 분산이 고정된 Gaussian distribution를 자주 사용한다. 

 

이제 reverse diffusion process를 생각해보자. reverse diffusion process 역시 diffusion process로 다음과 같은 reverse-time SDE로 나타낼 수 있다.

위 SDE에 score가 포함된 것을 알 수 있는데, 우리는 reverse-time SDE를 풀기 위해 score를 구할 줄 알아야 한다.

$ \nabla_x \log p_t(x)$를 구하기 위해 $s_{\theta}(x, t)$를 아래 식을 통해 학습해야 한다.

이 식은 denoising score matching 방법을 사용했는데, sliced score matching이나 finite-difference score matching 사용도 가능하다.

여기서 $\lambda : [0, T] \rightarrow \mathbb{R_{>0}}$는 positive weighting function이며, $x(0) \sim p_0(x)$, $x(t) \sim p_{0t}(x(t)|x(0))$이다. 충분한 데이터와 모델 capacityr가 있다면 score model은 optimal solution에 수렴할 것이다. 앞서 SMLD와 DDPM에서 살펴보았던 것 처럼 $\lambda \propto \frac{1}{\mathbb{E} \left[ \left\|\nabla_x(t) \log p_{0t}(x(t) \mid x(0)) \right\|_2^2 \right]}$와 같이 고르면 된다. 

 

또한 위 식을 풀기 위해서는 transition kernel $p_{0t}(x(t)|x(0))$를 알아야 하는데, $f(\cdot, f)$가 affine 형태면 transition kernel은 항상 Gaussian이며, 평균과 분산 또한 closed-form으로 알려져있다. 또한 좀 더 일반적인 SDE의 경우 Kolmogorov's forward equation으로 $p_{0t}(x(t)|x(0))$을 구할 수 있다. 혹은 sliced score matching 방법으로 $p_{0t}(x(t)|x(0))$ 계산을 우회할 수도 있다. 

 

Examples : VE, VP, sub-VP SDEs

SMLD의 perturbation kernel은 아래와 같이 나타낼 수 있다.

위 식에서 $N \rightarrow \inf$인 경우를 생각해보면 다음과 같은 SDE로 표현된다.

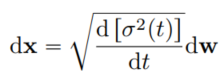
위 SDE의 variance는 $t$가 커짐에 따라 explode한다. 따라서 이 논문에서는 위 식을 Variance Exploding(VE) SDE라고 부른다. 

DDPM 의 perturbation kernel은 아래와 같이 나타낼 수 있다.

위 식에서 $N \rightarrow \inf$인 경우를 생각해보면 다음과 같은 SDE로 표현된다.

 

위 SDE의 variance는 $t$와 무관하게 variance가 일정하다. 따라서 이 논문에서는 위 식을 Variance Preserving(VP) SDE라고 부른다. 

Sub-VP SDE는 이 논문에서 제안한 새로운 타입의 SDE로 likelihood 관점에서 좋은 성능을 보인다. 식은 아래와 같다.

Sub-VP SDE는 같은 $\beta$와 initial distribution을 가정했을 때, VP SDE의 variance보다 항상 작다. 

 

VE, VP, sub-VP SDE 모두 affine drift coefficients이므로 perturbation kernels $p_{0t}(x(t)|x(0))$도 모두 Gaussian이며, closed-form으로 계산가능하다. 이러한 성질은 score 학습을 용이하게 한다. 

 

Solving The Reverse SDE

score-based model $s_{\theta}$를 학습한 뒤, $s_{\theta}$는 reverse-time SDE를 만들고 샘플을 생성하는데 사용된다. 

 

✔️ numerical SDE solver(Euler-Maruyama method, stochastic Runge-Kutta methods)를 이용해 reverse-time SDE를 풀어 샘플을 생성할 수 있다.

✔️ DDPM에서 제안된 샘플링 방법인 Ancestral sampling을 사용할 수도 있으나, 새로운 SDE에서 sampling rule을 도출하는 것은 어려울 수 있다.

✔️ 이 논문에서 제안한 reverse diffusion sampler를 사용할 수 있다.(설명은 아래 더보기 참고)

reverse diffusion sampler : 아래 (46)번 식을 이용해 $f$와 $G$에 각각 함수를 대입하여 샘플링한다.

predictor-corrector(PC) samplers

일반적인 SDE와 달리 우리에게는 score-based model $s_{\theta}$가 있으므로, Langevin MCMC나 Hamiltonian Monte Carlo와 같은 score-based MCMC기법을 사용해 $p_t$를 직접 샘플 추출하고 numerical SDE solver의 solution을 보정할 수 있다. 이 방법을 논문에서는 predictor-corrector(PC) samplers라고 부른다. 

 

predictor-corrector(PC) samplers

predictor : numerical SDE solver

corrector : score-based MCMC approach 

 

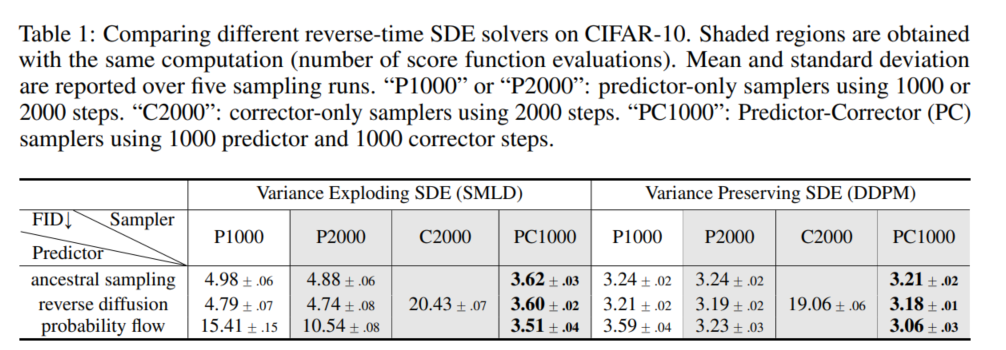
PC sampler를 SMLD와 DDPM 모델에서 테스트 했으며, 원래의 objective function을 사용해 훈련했다. 이는 PC sampler가 고정된 수의 노이즈 스케일로 훈련된 score-based model들과 호환 가능하다는 사실을 보여준다. 아래 실험결과에서 보여주듯 reverse-diffusion sampler가 Ancestral sampling보다 뛰어나며 PC sampler를 사용하는 것이 predictor만 사용하거나 corrector만 사용하는 것보다 성능을 높인다.

Probability Flow and Connection To Neural ODEs

score-based model은 또 다른 방법을 이용해 reverse-time SDE를 풀 수 있는데, 그것이 바로 Probability flow ODE 방법이다. 모든 diffusion process에 대해 이에 대응하는 SDE와 동일한 marginal probability density $\{ p_t(x) \}_{t=0}^{T}를 갖는 deterministic process가 있으며, 아래와 같은 ODE로 표현 가능하다.

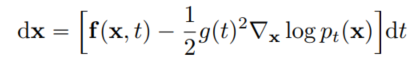
이 ODE를 Probability flow ODE라고 부르며, 이 ODE는 score를 알면 계산이 가능하다. 스코어 함수가 시간에 따라 변하는 socre-based model에 의해 근사될 때, 이는 neural ODE의 한 예가 된다.

 

장점

1. Exact likelihood computation : neural ODE와 연관지어 생각해보면, 우리는 instantaneous change of variable formula를 통해 density를 계산할 수 있다. 이는 어떠한 input data에 대해서도 exact likelihood를 계산할 수 있게 한다.
2. Manipulating latent representations : PF ODE를 적분하면 어떤 데이터 포인트 $x(0)$도 latent space $x(T)$로 인코딩할 수 있다. 디코딩은 reverse-time SDE에 대응하는 ODE를 적분해 수행할 수 있다. 이렇게 얻은 latent representation을 통해 image editing(interpolation, temperature scaling)등을 수행할 수 있다.
3. Uniquely identifiable encoding : 여기서 얻은 encoding은 uniquely identifiable하기 때문에, 충분한 훈련데이터와 모델 용량, 정확도가 주어지면 입력에 대한 인코딩이 데이터 분포에 의해 고유하게 결정된다. 이는 forward SDE에 학습 가능한 파라미터가 없고, 이와 관련된 PF ODE가 완벽하게 추정된 score를 사용하면 동일한 경로를 제공하기 때문이다.
4. Efficient sampling : neural ODE와 마찬가지로 서로 다른 $x(T) \sim p_T$에서 시작해서 $x(0) \sim p_0$를 샘플링할 수 있다. fixed discretization strategy를 corrector와 함께 사용하면 경쟁력 있는 샘플을 사용할 수 있다. blackbox ODE solver를 사용하면 높은 품질의 샘플을 생성할 수 있을 뿐만 아니라, 효율성을 위해 정확성을 조절할 수 있다. 오차 허용 범위를 크게 설정하면 함수 평가 횟수를 90%이상 줄일 수 있으나, 샘플의 시각적 품질에는 영향을 미치지 않는다. 실험 결과는 아래 그림을 참고하면 된다.

Architecture Improvements

VE SDE의 최적의 architecture NCDN++와 VP SDE의 최적 architecture DDPM++의 실험결과는 아래 표에 제시되어 있다. (NCSN++와 DDPM++는 저자가 최적의 NCSN와 DDPM setting을 찾아 명명한 것이다. 자세한 내용은 이 논문의 부록 H 부분을 참고하면 된다.)

 

Controllable Generation

$p_0$뿐만 아니라 $p_0(x(0)|y)$에서도 데이터 샘플을 생성할 수 있다. 만약 $p_t(y|x(t))$가 알려져 있다면, 순방향 SDE가 주어져 있을 때, 우리는 $p_T(x(T)|y)$로부터 샘플링하여 conditional reverse-time SDE 역시 다음 식을 통해 샘플링할 수 있다.

일반적으로 $ \nabla_x \log p_t(y \mid x(t))$에 대한 추정값이 주어지면, 위 식을 사용해 reverse-time SDE를 해결할 수 있다. 일부의 경우 $\log p_t(y \mid x(t))$를 학습하기 위해 별도의 모델을 훈련하고 그 기울기를 계산할 수 있다. 부록에서는 이러한 추정을 별도의 보조 모델을 훈련하지 않고도 얻는 방법을 제시한다. 

 

class-conditional generation, image imputation, colorization에 이용할 수 있으며, $y$가 클래스 레이블을 나타낼 때, time-dependent classifier $p_t(y|x(t))$를 훈련할 수 있다. 

 

Reference

[1] https://dlaiml.tistory.com/entry/Score-based-Generative-Models%EA%B3%BC-Diffusion-Probabilistic-Models%EA%B3%BC%EC%9D%98-%EA%B4%80%EA%B3%84