Denoising Score Matching(DSN) 논문 리뷰(A Connection Between Score Matching and Denoising Autoencoders)

Score-based models에 대해 공부하다가 Denoising Score matching 내용이 나와 근본 논문을 살펴보고자 2011년 AISTATS에 게재된 'A Connection Between Score Matching and Denoising Autoencoders'를 정리하게 되었다.

 

논문의 주요 수식 위주로 요약해보고자 한다.

 

※ 읽기에 앞서 score function 관련 내용에 대한 사전 지식이 필요하다. 관련 내용은 Score-based models 포스팅을 통해 확인할 수 있다.

 

Notation

Parzen density estimate에 대한 설명)

chatgpt가 해준 설명과 블로그 글을 읽어보면 이해가 된다!

 

Denoising Autoencoders(DAEs)

Denoising autoencoders (DAEs) are a simple modification of classical autoencoder neural networks that are trained not to reconstruct their input but rather to denoise an artificially corrupted version of their input (Vincent et al., 2008, 2010)

 

DAE는 AutoEncoder가 쉽게 항등 매핑을 학습할 수 있는 반면, 노이즈가 포함된 input을 reconstruct해야 하기 때문에 더 유용한 특징을 추출하게끔 학습된다. 실제로 DAEs는 AE에 비해 상당한 성능의 발전을 가져왔다. 이 논문에서는 심플한 버전의 DAE를 생각해볼 것이다. 

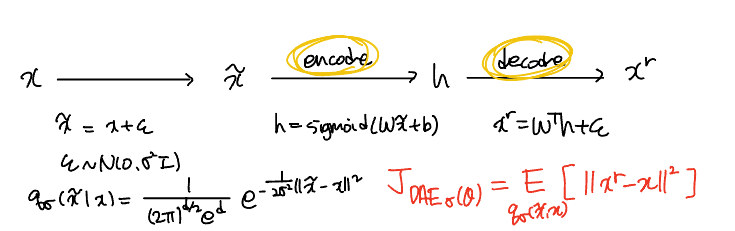
자세한 구조는 논문 참고

Score Matching

다음과 같이 density model $p(x; \theta)$를 설정하고 $\theta$를 잘 학습해 원하는 데이터의 확률 분포를 추정해보자.

여기서 $E$는 energy function이라고 하며, 우리는 log density의 gradient를 score라고 정의한다.

score

(1)  $J_{ESM_q}(\theta)$ : Explicit score matching

우리의 목표는 $\theta$를 잘 학습시켜 score function과 true log distribution의 gradient가 일치하기를 바란다.

Explicit score matching(ESM)

하지만 우리는 true distribution $q$를 모르기 때문에 $J_{ESM_q}(\theta)$를 최적화시킬 수 없다.

※ score function은 partition function $Z(\theta)$를 포함하고 있지 않다.

 

(2)  $J_{ISM_q}(\theta)$ : Implicit score matching 

Explicit score matching식은 Implicit score matching식으로 변환될 수 있으며, 더 이상 explicit score target $q$이 식에 포함되지 않는다. 

$q$와 $\phi$가 weak regularity conditions를 만족하면 우리는 $J_{ISM_q}(\theta)$과  $J_{ESM_q}(\theta)$가 사실상 동일한 optimization objective임을 증명할 수 있다.

weak regularity conditions

(3)  $J_{ISM_{q_0}}(\theta)$ : Finite Sample Version of Implicit Score Matching

우리는 주어진 샘플셋 $D_n$에서 계산을 수행하기 때문에, Finite Sample 버전의 $J_{ISM_q}(\theta)$를 아래와 같이 계산해야 한다.

 $J_{ISM_{q_0}}(\theta)$ 는 n이 무한으로 발산함에 따라  $J_{ISM_{q}}(\theta)$로 수렴한다.  

 

따라서 다음과 같은 equivalence 관계로 나타낼 수 있다.

다만 우리는 무한한 n에 대해서는 계산할 수 없으며, 유한한 샘플에 대한  $J_{ISM_{q_0}}(\theta)$에 대해서는 아는 바가 없다. 이에 Kingma와 LeCun은 2010년 regularized version of  $J_{ISM_{q_0}}(\theta)$를 제시했다.

 

결론) regularity condtion은 만족하는 $q$에 대해 다음 equivalence가 만족한다.

Linking Score Matching to the Denoising Autoencoder Objective

이번에는 true distribution $q$ 대신 Parzen window density estimator $q_{\sigma}(\tilde{x})$에 대해 생각해보자. Explicit Score matching을 통해 다음과 같은 objective를 얻을 수 있다.

아래 조건을 만족하면,  $J_{ISM_{q_{\sigma}}}(\theta)$와 $J_{ESM_{q_{\sigma}}}(\theta)$는 사실상 동일한 obejctive이다.

 

(1) Matching the Score of a Nonparametric Estimator

 다만 여기서 주목할 점은 $\sigma$가 0에 가까워지면 equivalance가 깨지는데, 이유는 $q_{\sigma}$가 더이상 regularity condition을 만족하지 않고, $J_{ESM_{q_{\sigma}}}(\theta)$은 계산이 불가능하기 때문이다.( $J_{ISM_{q_{\sigma}}}(\theta)$는 well behaved!)

 

(2) Denoising Score Matching

clear data $x$에 대해 noise를 추가한 data를 $\tilde{x}$라고 하자. $(x, \tilde{x})$의 joint density는 다음을 만족한다.

이때, denoising score matching(DSM) objective를 다음과 같이 정의하자.

gaussian kernel 사용시 다음과 같은 식을 얻는다.

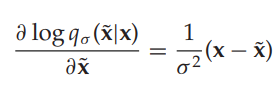
위 objective는 Appendix에 있는 증명에 의해  $J_{ESM_{q_{\sigma}}}(\theta)$와 동치이다. 

(3) An Energy Function that yields the denoising autoencoder objective

처음에 정의한대로 $p(x; \theta)$와 DAE는 다음과 같이 정의한다.

증명과정은 생략하면 우리는 다음을 얻을 수 있다.

증명)

Discussion

앞에서의 증명을 종합해보면 다음과 같은 결론을 얻을 수 있다.($\sigma > 0$)

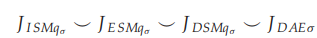
즉, DAE를 학습하는 것은 energy function on Parzen density estimate $q_{\sigma}$를 이용해 SM를 수행하는 것과 동일하다.